El-Gabbas A. & Dormann C. F.: Improved species-occurrence predictions in data-poor regions: using large-scale data and bias correction with down-weighted Poisson regression and Maxent. Ecography DOI: 10.1111/ecog.03149.
Appendix 1: Supplementary figures and tables Table A1: The estimated optimum combination of Maxent’s feature classes (FC) and Regularization Multiplier (RM) for each species and bias model type. Combinations with highest mean testing-AUC on
5-folds spatial-block cross-validation were selected. All the analyses were performed using modified code from the ENMeval package in R (Muscarella et al., 2014). See main text for more information. Species Environment-only Accessibility Effort a
Feature classes (FC): L linear; Q quadratic; H hinge; P product; and T threshold. For more details see Elith et al. 2011. b RM is a global multiplier to all individual regularization values; for more details see the main text and Muscarella et al.
(2014). Table A2: Estimated best values to run the elastic-net models (DWPR approach) for different species and bias models. For details, see main text. Species Environment-only Accessibility Efforts LASSO RIDGE Fig. A1: Map of all non-marine
GBIF-records. There are clear signs of sampling bias inherited in the GBIF database, disallowing the direct use of these records to run SDMs, unless action is taken to correct for sampling bias. GBIF-records are biased mainly towards Western
Europe, with sparse locations across Africa, Asia, and Eastern Europe. Areas shown in white represent pixels without any records (the majority of North and central Africa, Arabia, and eastern Europe). Clearly errorneous records were excluded
before plotting this map.Fig. A2: Left: Map of all GBIF bat records (accessed date: April 2015) per a grid of 20 × 20 km2.Right: All records available of the study species, collected either from the literature (blue points) or GBIF (red points).
Both maps show large collection gaps. Fig. A3: Per-species study area: An example of how the ‘per-species’ study area was determined (here for Asellia tridens). The dashed red line indicates the species extent of occurrence (minimum convex
polygon); the solid red line shows the buffer used (1000 km), and the dashed green line indicates the study area used. Fig. A4: Variables selection: Pearson correlation coefficient between each pair of the final covariates; see Appendix 3 for more
information. Fig A5: Per-species number of backgrounds: Objectively determining the adequate number of background ‘quadrature’ points to be used in GLM and elastic-net models (see main text and Renner et al., 2015). DWPR-GLM models (for each
species, here: Asellia tridens) were repeated 25 times (each time, with a different random sample from the background) with progressively increase the number of background points (from 5000 to 500,000); and for each model, the log-likelihood value
is calculated and plotted. The number of backgrounds at which the likelihood converges (i.e. no much benefit of using a higher number of backgrounds) is, visually, selected to run the final models. Here, no much improvement in the log-likelihood
beyond 300,000 background points (out of 557,800 total available background points) and so we used it for this species. Fig. A6: Determining the best value to run the elastic-net model for Nycticeinops schlieffeni (effort model). Eleven values
ranging from zero (ridge) to one (lasso), with an increment of 0.1, were used to run 11 models on cross-validation. For each value of , glmnet ran many models on a range of -values (estimated from the data; x-axis) and measure the mean
cross-validation error (cvm) (here: Poisson deviance; y-axis). The value with the lowest cvm is used further while predicting (vertical dotted lines, with colours correspond to the value used). Here, an value of 0.6 is shown to have the lowest cvm
and so used further. For more details, see Table A2 and the main text. Fig. A7: Kendall’s correlation between (per-species and modelling algorithm) mean AUC evaluated on spatial-block cross-validation and independent evaluation in Egypt. Each
point represents the mean of 100 AUC values, with different symbols for each species. Colours represent different modelling algorithm used. ‘M’ indicates the overall mean for each modelling algorithm. Panel (a) shows the correlation for the
environment-only models (no bias correction). Panels (b-c) represent the accessibility model, without and with correcting for sampling bias, respectively. Panels (d-e) represent the effort model, without and with correcting for sampling bias,
respectively. Kendall’s correlation coefficients (and their p-values) are reported in each block. Grey solid line represents the equality line. AUC performed on cross-validation were, on average, higher than AUC in Egypt. However, there is
moderate correlation between bias-free evaluations on either scale. Fig. A8: Equivalent results to Fig. A7, for TSS evaluation. Fig A9: Boxplots of the raw cross-validation evaluation (100 values) without (modelling evaluation; a and c) and with
(bias-free evaluation; b and d) correction for sampling bias; either using AUC (a - b) or TSS (c - d); see Appendix 6 for more information. Horizontal panels show results for different modelling algorithm, while the vertical panels show different
bias models. Panels a & c show results for the environment-only model (without any bias manipulation) and bias-accounting models (accessibility and effort models) without correcting for sampling bias. However, panels b & d compare results for the
environment-only model and bias-accounting models (accessibility and effort models) after correcting for sampling bias (see main text; for effort models, plots show evaluations either conditioning the predictions on a value of zero or the maximum
relative sampling effort of training presences). Species are in ascending order according to their number of occupied pixels at cross-validation scale (with numbers represent the species; see Table 1 for full species names). Fig. A10: Similar to
Fig. A9, but showing results of independent evaluation in Egypt. Evaluation metrics are calculated in Egypt using mean predictions (of 5-folds cross-validation) in Egypt along with entirely independent species records from Egypt (not used to run
any of the models). Species are in ascending order according to their number of occupied pixels in Egypt (with numbers represent the species; see Table 1 for full species names). Fig. A11: Species mean TSS calculated either on cross-validation (a
- b) or in Egypt (c - d), either without (modelling evaluation; a & c) or with (bias-free evaluation; b & d) sampling bias correction (for details, see Appendix 6). Each species is represented by different symbols (similar to those shown in Fig.
A7; numbers represent species used, see Table 1). Red lines indicate the overall mean TSS at each modelling algorithm and bias models applied. Fig. A12: Kendall’s correlation of the per-species mean TSS between different pairs of modelling
algorithms (same as Fig. 2 in the main text, but for TSS). Each species is represented by different symbol (similar to those of Fig. A7) with different colours for different bias models applied (using predictions of environment-only model and
bias-free prediction of accessibility and effort model). ‘M’ indicates the overall mean evaluation. First row represents mean spatial-block cross-validation evaluation, while the second is for independent evaluations in Egypt. Fig. A13: Values of
bias variables at presences and available locations (backgrounds), at the per-species study area (A) or at local scale ‘Egypt’ (B). Rows correspond to different species, with numbers indicates the species (see Table 1), and columns represent bias
variables of the accessibility model (distances to roads, cities, and protected areas) and effort model (relative bats’ sampling intensity). For each species, values at presence locations are indicated with black, and values at pixels unoccupied
by the species are shown in grey. Most of the species are recorded from closer to roads and cities (and to some extent, the protected areas), and unexpectedly at low to moderate sampling efforts. Fig. A14: AUC scores calculated the default way
(using all available testing backgrounds – y-axis) versus using a fixed ratio between testing presences and backgrounds (test-data prevalence = 1:20 – x-axis). (A) shows the raw outputs of 5-folds cross-validation. (B) shows the per-species mean
AUC on cross-validation. Different colours represent the three bias models applied (environment-only, accessibility, and efforts). Fig. A15: The predicted distribution of Otonycteris hemprichii (mean of 5-folds cross-validation), using different
modelling algorithms (rows) and bias models (columns). Maps were scaled between zero and one, as different modelling algorithms do not have the same scale, with blue colour indicates higher predicted relative intensity. (A) shows cropped predicted
distribution of Otonycteris hemprichii (the same as Fig. 5) to Egypt. Grey points (in the top left panel) represents available records used for indepenent evaluation presences in Egypt. In Fig. 5 of the main text, extreme values (> 0.9995 quantile
of predicted values) were replaced with their next smaller value to improve map visualization, as GLM and elastic-net models sometimes yielded extreme values. Maps in (B) are equivalent to maps in Fig. 5, without any extreme values manipulation
(using the linear scale), demonstrating the difficulty of visualizing the predicted patterns in the existence of extreme values; see main text for more details. Fig. A16: The reported and predicted distribution of Rhinolophus mehelyi (Maxent). The
2nd to the 4th panels show predictions from environment-only model and bias-free prediction of accessibility and effort models, respectively. Arrows represent regions which gain higher predicted values after correcting for sampling bias (such as
central Turkey or the Algerian Atlas). Predictions at these areas are of higher uncertainty (lower congurrence) and field validation is probably required to confirm the species existence. The lighter the colour, the more suitable the location.
Appendix 3: Variables selection List of initial covariates investigated for correlation/multi-collinearity and transformation applied. Final list used to run the model is marked in grey. Variable Transfo- rmation VIF 10 | cor | 0.7 GVIF 3 Alt a
Altitude yes yes yes Bio1 Annual mean temperature ^2 Bio2 Mean diurnal range (mean of monthly (max temp - min temp)) yes yes yes Bio3 Isothermality (Bio2/Bio7) (* 100) Bio4 Temperature seasonality (standard deviation *100) yes yes yes Bio5 Maximum
temperature of warmest month Bio6 Minimum temperature of coldest month Bio7 Temperature annual range (Bio5-Bio6) Bio8 Mean temperature of wettest quarter ^2 yes yes yes Bio9 Mean temperature of driest quarter ^2 yes yes yes Bio10 Mean temperature
of warmest quarter ^2 Bio11 Mean temperature of coldest quarter yes yes Bio12 Annual precipitation sqrt Bio13 Precipitation of wettest month yes Bio14 Precipitation of driest month yes yes yes Bio15 Precipitation seasonality (coefficient of
variation) yes yes yes Bio16 Precipitation of wettest quarter sqrt Bio17 Precipitation of driest quarter Bio18 Precipitation of warmest quarter yes yes Bio19 Precipitation of coldest quarter log yes yes yes PET b Potential evapotranspiration AI b
Aridity index sqrt AET c Actual evapotranspiration sqrt SWB c Soil-water balance sqrt NDVI_Max d Maximum NDVI (Normalized Difference Vegetation Index) NDVI_Min d Minimum NDVI yes yes yes NDVI_Mean d Mean NDVI NDVI_Range d Range NDVI (maximum –
minimum) NDVI_SD d Standard deviation of NDVI yes yes yes EVI_Max d Maximum EVI (Enhanced Vegetation Index) EVI_Min d Minimum EVI yes EVI_Mean d Mean EVI yes EVI_Range d Range EVI (maximum - minimum) yes EVI_SD d Standard deviation of EVI a
WorldClim : WorldClim provides a global dataset for the elevation and 19 bio-climatic variables interpolated from global monthly temperature and precipitation recordings from weather stations (Hijmans et al. 2005). Tiles for the overall study area
were downloaded at 30 arc-seconds resolution (~1 km near the equator; using the raster R_package), then projected to Mollweide equal-area projection at 5 × 5 km2 resolution. The high resolution of 30 arc-seconds was preferred over the 2.5 arc
minutes (~5 km near the equator) in order not to lose much information while re-projecting. Instead of interpolation (assigning a value for the new pixel equals to the mean of the nearest three points at the original projection), a different
approach was employed. First, a template grid covering the study area at the equal-area projection (5 × 5 km2) was prepared. Then, pixels of the original variables (at 30 arc-seconds resolution) were converted into centroid points (at the original
projection: WGS-1984), then projected into Mollweide projection, then these points were rasterized using the mean value (or other relevant function for some variables; e.g. maximum for Bio5) of the points that spatially fall within each cell of
the template grid. The same approach was used to prepare all other covariates used in this study. b Global Potential Evapotranspiration (Global-PET) & Global Aridity (Zomer et al. 2007, 2008) : available at the global scale at a resolution of 1
km, and were prepared based on models that use data from WorldClim as inputs. Global Actual Evapotranspiration (Global-AET) & Global Soil-Water-Balance (Global-SWB) (Trabucco & Zomer 2010) : available at the global scale at a resolution of 1 km,
and are prepared based on WorldClim and Global-PET database as primary input. d NDVI (Normalized Difference Vegetation Index) & EVI (Enhanced Vegetation Index) (Didan, 2015) : map tiles for the whole study area were downloaded (and merged) for the
period from 18/2/2000 to 22/3/2015 each 16 days (MODIS product: MOD13A2 – resolution: 1 km) using the MODIS R package (Mattiuzzi, 2014). Summary maps (maximum, minimum, mean, range, and standard deviation) across the whole period (for NDVI & EVI)
were produced at the original MODIS scale/projection using a python code in ‘ArcGIS’ as this was memory intensive to perform in raster package of R. Each of the summary layers were then projected into the equal-area projection at 5 × 5 km2
resolution. Possible covariate transformations were investigated, trying to keep some degree of uniform distributions across the range of each covariate (following: Dormann 2011). For some covariates, no transformation was effective, and they were
kept untransformed. • Variable selection: Multicollinearity amongst the potential covariates )covering the total study area( was assessed, maintaining highest GVIF (Generalized Variance Inflation Factor) 3 (Zuur et al. 2009) [which is equivalent,
in our case, to maintaining a highest absolute correlation coefficient between each pair of covariates 0.6 and highest VIF (Variance Inflation Factor) 10]. This was also checked for each species’ study area. Aridity-related covariates
(actual/potential evapotranspiration, aridity-index, and soil-water-balance) were all excluded as they show high collinearity with other WorldClim covariates; unsurprisingly as they were derived from models that use WorldClim data as input. Out of
tensummary vegetation-related covariates, two NDVI covariates were used further: the cumulative minimum and the standard deviation NDVI. They reflect indices of minimum biomass and variability of vegetation-cover across the study area,
respectively. Appendix 4: Per-species spatial-block cross-validation For each species, a different spatial-block cross-validation structure was used to run SDMs. Pixels across the study area were aggregated into larger blocks (each of 20 × 20
cells = 100 × 100 km2), and blocks were distributed into cross-validation folds. Presences and backgrounds in each block were used together either as training or testing (Fithian et al. 2015). The blocks were not distributed into cross-validation
folds randomly, as this would have yielded highly unbalanced numbers of presence-locations across spatial folds. Instead, we balanced the number of presence locations at different folds by calculating their numbers at each block; the top 5 blocks
were then, sequentially, randomly assigned to five folds (to avoid that the first fold always has the highest number of presences). To avoid high variability in the environmental space between folds and minimise much extrapolation while predicting
to the left-out-fold, blocks without any species records were distributed into folds depending on a mean index of their similarity to the overall study area: using the Multivariate Environmental Similarity Surfaces ‘MESS’. MESS was proposed by
Elith et al. (2010) to identify areas of novel climates by comparing future (or past) climate to those used to run the models, as the interpretation of future projections at these locations should be considered with caution. We calculated the
MESS-score for each pixel (and a mean value for each block) quite differently from how it was proposed in the first place: we measured the environmental similarity of each pixel to all available pixels in the study area (using the ‘dismo’
package). The original application of MESS gives most dissimilar locations more negative values (Elith et al. 2010); however here we expect no negative values as there is no climates novelty. Blocks without any presence locations are sorted in
descending order (depending on their average MESS value), and then the highest five blocks were distributed randomly into different folds. This was repeated for all blocks until all blocks were distributed to different folds. An example of how
spatial-block cross-validation applied for Asellia tridens. Different colours represent how different blocks are distributed into cross-validation folds. Blue points represent the species known distribution from outside Egypt. For each per
species’ study area, a different blocking structure was prepared, to balance the number of presence locations and environmental variability at different cross-validation model runs. Appendix 5: Sampling-effort model Data for closely related
species (bats/non-marine mammals) were downloaded from GBIF (The Global Biodiversity Information Facility – April 2015) and used (along with available focal species records: Tables 1 & A1) to model the relative sampling intensity (surveying
effort) of bats/mammals. The prediction map of this model was used as bias covariate in the ‘Effort models’ (see main text, Fig. 1, bottom right). Records were assessed before usage (records with missing coordinates or with clear errors were
excluded: e.g. missed latitude or longitude / equal latitude and longitude / records in the sea or the ocean / potentially swapped latitude and longitude), resulting in a total of 435,458 bat records / 2,039,158 non-marine mammal records (maps
below). GBIF records (for both bats and mammals) show high bias towards the Western Europe compared to any other area in the study area, followed by scattered locations elsewhere (mostly close to the main cities, water bodies, populated areas, or
seemingly a result of a mammals atlas mapping activity in southwest Africa). The majority of Africa and eastern Europe to western Asia is extremely under-represented in GBIF, with huge gaps in North Africa and Arabia. Maps show the number of GBIF
records of non-marine mammals (left) and bats (right) per a grid of 20 × 20 km2 (accessed date: April 2015). Initial trials for modelling the sampling effort were done using DWPR-GLM (Down-Weighted Poisson Regression) and Maxent (both using
PPM-like approach; see main text); without much difference in the resulted prediction pattern (although Maxent model ‘using default feature classes and regularization multiplier’ shows, visually, an over-fitted spatial pattern). DWPR-GLM model was
chosen to run at 5×5 km2 equal-area projection: all the bats/mammals presence locations as the response (without duplicates removal) and using different covariate set than the environmental variables used to run the species SDMs (Merow et al.
2016) Terrain roughness (represented here as a per-pixel standard deviation of altitude): Altitude maps from WorldClim was downloaded at of 30 arc-seconds resolution [~1 km near the equator], then projected as points in Mollwide equal-area
projection. The points were then converted to a raster (rasterized), representing the standard deviation of the elevation values located at any target pixel at the resolution of 5 × 5 km2; Distance to main cities : the Euclidean distance between
the centroid of each pixel and the nearest human settlement; Distance to main roads : the Euclidean distance between the centroid of each pixel and the nearest road (Source: Global Roads Open Access Data Set ‘gROADS’); Population count : global
population count in 2000; Protection status : a binary variable indicating the protection status of each pixel [source: The world Database of Protected Areas:]. The overall pattern of the predicted sampling effort for both bats and mammals were
roughly similar (maps below), so the prediction from the bats sampling effort model was used further (as bias covariate in the effort model). It represents the overall relative abundance of bat species sightings per unit area (based only on
non-climatic covariates). The predicted sampling intensity of sightings (sampling effort) for all bats (left) and non-marine mammals (right) using the DWPR-GLM (Down-Weighted Poisson Regression) model. Appendix 6: Mixed effect model analysis of
evaluation Mixed Models formula: Evaluation metric ~ Modelling algorithms * Bias models + total number of training presences (training data) + number of pixels in the study area (total area) + (1 | species) Evaluation metric continuous variable
for either AUC or TSS either using mean cross-validation evaluation (AUCcv/TSScv) or independent evaluation in Egypt (using mean prediction of 5-folds cross-validation to Egypt and independent testing data from Egypt) Modelling algorithms:
categorical variable indicating the modelling algorithm used (elastic net / GLM / Maxent) Bias models: 1. Modelling evaluation: evaluation of environment-only model (base line; no bias manipulation) is compared with those of bias-accounting models
(accessibility and effort), without correction for sampling bias [without fixing bias variables at any values]. 2. Bias correction evaluation: evaluation of environment-only model (base line; no bias manipulation) is compared with those of bias
accounting models (accessibility and effort), after correction for sampling bias [accessibility bias variables are set to zero, while the effort bias variable is set to either zero or the maximum estimated effort of the target species’ presence
records; see below]. Species: random factor; categorical variable for the species. Modelling Evaluation – Without Bias correction Variance explained (sum of squares) AUC TSS Mean cross-validation Egypt evaluation Mean cross-validation Egypt
evaluation Bias models Model techniques Bias models * Model techniques Total number of training presences Study area Parameter estimates (Mixed models summary) Bias correction evaluation – using bias-free predictionsAfter correcting for sampling
bias, initial trials show that using either value for fixing the effort bias covariate produce very similar evaluations (however, Maxent models show quite lower AUCs using the maximum effort value of training presences than for fixing at zero;
Fig. 3), so we limited further analyses to effortMax.When predicting with fixed values for the bias-covariates, modelling algorithms were most important for explaining variability of cross-validations, followed by sampling-bias models and then
their interaction (for evaluation in Egypt highest variability was explained by the sampling-bias models, followed by the modelling algorithm, and then their interaction). Again, the number of training presences and study area were much less
important (and the sign of their effects resembles those of modelling evaluation). The accessibility model had lower AUC compared to the two other sampling-bias models in all comparisons (Fig. 3). On cross-validation, bias-accounting models had
lower AUC-values compared to the environment-only model (very little difference between environment-only and effort model for GLM; Fig. 3a). For evaluations in Egypt, environment-only and effort model were hardly different (effort model had lower
AUC for Maxent ; Fig. 3b).Variance explained (sum of squares) AUC TSS Mean cross-validation Egypt evaluation Mean cross-validation Egypt evaluation Bias models Model techniques Total number of training presences Study area Parameter estimates
(Mixed models summary) AUC TSS Mean cross-validation Egypt evaluation Mean cross-validation Egypt evaluation(Intercept) [env-only/ elastic net] Estimated differences in the least square means AUC TSS Mean cross-validation Egypt evaluation Mean
cross-validation Egypt evaluation Modelling techniques Supplementary references Didan K (2015): MOD13A2 MODIS/Terra Vegetation Indices 16-Day L3 Global 1km SIN Grid V006. NASA EOSDIS Land Processes DAAC. Dormann CF (2011): Modelling Species’
Distributions. In Fred J, Hauke R, Broder B (Eds.): Modelling Complex Ecological Dynamics. Berlin, Heidelberg: Springer Berlin Heidelberg, pp. 179–196. Elith J, Kearney M, Phillips S (2010): The art of modelling range-shifting species. Methods in
Ecology and Evolution 1: 330–342. Fithian, W., Elith, J., Hastie, T., Keith, D.A. & O'Hara, R.B. (2015). Bias correction in species distribution models: pooling survey and collection data for multiple species. Methods in Ecology and Evolution, 6,
424–438. Friedman J, Hastie T, Tibshirani R (2010): Regularization Paths for Generalized Linear Models via Coordinate Descent. Journal of Statistical Software, 33(1), 1-22. URL: http://www.jstatsoft.org/v33/i01/. Hijmans RJ, Cameron SE, Parra JL,
Jones PG, Jarvis A (2005): Very high resolution interpolated climate surfaces for global land areas. In Int. J. Climatol. 25 (15), pp. 1965–1978. Merow C, Allen JM, Aiello-Lammens M & Silander JA (2016): Improving niche and range estimates with
Maxent and point process models by integrating spatially explicit information. Global Ecology and Biogeography, 25, 1022–1036. Mattiuzzi M (2014): MODIS: MODIS acquisition and processing. R package version 0.10-17/r484.
(https://R-Forge.R-project.org/projects/modis/) Renner IW, Elith J, Baddeley A, Fithian W, Hastie T, Phillips SJ., et al. (2015): Point process models for presence-only analysis. Methods in Ecology and Evolution 6: 366–379. Trabucco A, Zomer RJ
(2010): Global Soil Water Balance Geospatial Database. CGIAR Consortium for Spatial Information. Published online, available from the CGIAR-CSI GeoPortal at: http://www.cgiar-csi.org. Zomer RJ, Bossio DA, Trabucco A, Yuanjie L, Gupta DC, Singh VP
(2007): Trees and Water: Smallholder Agroforestry on Irrigated Lands in Northern India. Colombo, Sri Lanka: International Water Management Institute. pp 45. (IWMI Research Report 122). Zomer RJ, Trabucco A, Bossio DA, van Straaten O, Verchot LV
(2008): Climate Change Mitigation: A Spatial Analysis of Global Land Suitability for Clean Development Mechanism Afforestation and Reforestation. Agric. Ecosystems and Envir. 126: 67-80. Zuur AF, Ieno EN, Walker NJ, Saveliev AA, Smith GM (2009):
Mixed Effects Models and Extensions in Ecology with R. New York, NY: Springer New York.
El-Gabbas A. & Dormann C. F.: Improved species-occurrence predictions in data-poor regions: using large-scale data and bias correction with down-weighted Poisson regression and Maxent. Ecography DOI: 10.1111/ecog.03149. Ahmed El-Gabbas & Carsten
F. Dormann Department of Biometry and Environmental System Analysis, University of Freiburg, D-79106 Freiburg, Germany bat, Maxent, point-process model, presence-only data, species distribution modelling, sampling bias Running-title: Bias
correction for sparse presence-only data Abstract Species distribution modelling (SDM) has become an essential method in ecology and conservation. In the absence of survey data, the majority of SDMs are calibrated with opportunistic presence-only
data, incurring substantial sampling bias. We address the challenge of correcting for sampling bias in the data-sparse situations. We modelled the relative intensity of bat records in their entire range using three modelling algorithms under the
point-process modelling framework (GLMs with subset selection, GLMs fitted with an elastic net penalty, and Maxent). To correct for sampling bias, we applied model-based bias correction by incorporating spatial information on site accessibility or
sampling efforts. We evaluated the effect of bias correction on the models’ predictive performance (AUC and TSS), calculated on spatial-block cross-validation and a holdout data set. When evaluated with independent, but also sampling-biased test
data, correction for sampling bias led to improved predictions. The predictive performance of the three modelling algorithms was very similar. Elastic-net models have intermediate performance, with slight advantage for GLMs on cross-validation and
Maxent on hold-out evaluation. Model-based bias correction is very useful in data-sparse situations, where detailed data are not available to apply other bias correction methods. However, bias correction success depends on how well the selected
bias variables describe the sources of bias. In this study, accessibility covariates described bias in our data better than effort covariates, and their use led to larger changes in predictive performance. Objectively evaluating bias correction
requires bias-free presence-absence test data, and without them the real improvement for describing a species’ environmental niche cannot be assessed. Introduction Species distribution data often come in the form of presence-only, with information
on where species have been recorded, but no reliable information on where they have not, or where people have looked (Pearce and Boyce 2006). Museums, herbaria, personal collections, published literature, and citizen records are valuable sources
for presence-only data (Pearce and Boyce 2006, Newbold 2010), especially in developing countries where there is a lack of systematic nation-wide surveys. Some initiatives make such species sightings freely available: GBIF (the Global Biodiversity
Information Facility – see: http://www.gbif.org) collates global biodiversity data from different sources. One fundamental problem is that data are often incidental with no information on the sampling efforts and survey method used (Pearce and
Boyce 2006). They are biased taxonomically (towards larger, easy to detect, or more charismatic species groups; Newbold 2010), environmentally (less collection effort in areas with harsh environments), temporally (more in summer than winter), and
spatially (near populated places, roads, research institutes and protected areas; Phillips et al. 2009, Newbold 2010, Stolar and Nielsen 2015). For example, GBIF-data show huge differences in data contribution among countries (Supplementary
material Appendix 1, Fig. A1; on average, more from well-financed than from species-rich countries). Spatial bias is a particular concern for statistical analysis when it leads to environmental bias (Phillips et al. 2009), e.g. when large parts of
the environmental space remain unsampled (Merow et al. 2014). Species distribution models (SDMs) relate species occurrences to the environment to estimate habitat preference, and predict potential distribution and responses to climate change
(Phillips and Dudík 2008, Elith et al. 2011). Statistical analyses of presence-only data describe the environment at record locations relative to the background environment, making them more susceptible to sampling bias than presence-absence data
from dedicated surveys (Phillips et al. 2009, Fithian et al. 2015). However, such targeted survey-data are rare (Pearce and Boyce 2006), especially in developing countries, explaining why the majority of SDM applications uses presence-only data.
Presence-only data may produce sound models if they are efficiently corrected for sampling bias (Elith et al. 2011). Point-process models (PPM) have recently emerged as the most appropriate technique for presence-only data (Renner et al. 2015).
PPMs do not use background points as pseudo-absences (as in the naïve logistic regression; Fithian and Hastie 2013), but rather as quadrature points for estimating the spatial integral of the likelihood function, and hence require careful tuning
of its number (for details see, e.g., Warton and Aarts 2013). The response variable of PPMs is the density of species records per unit area (also called ‘intensity’), which should be proportional to the probability of occurrence (which can not be
estimated empirically using presence-only data without additional information; see: Fithian and Hastie 2013, Renner et al. 2015, Phillips et al. 2017). It is mathematically equivalent to methods already commonly used in ecology, e.g. Maxent and
some implementations of the generalised linear modelling framework, but differently efficient (Renner and Warton 2013, for details, see: Renner et al. 2015). Sampling bias has been addressed by ‘spatial filtering’ of presence locations (keeping
only a limited number of records within a certain distance) to dilute the effect of uneven sampling effort across the study area (e.g. Anderson and Raza 2010, Boria et al. 2014). Alternatively, others effectively use location of records from
related species as background points to have background points with the same bias as the species records (Elith and Leathwick 2007, 'target-group background': Phillips et al. 2009, see also: Ponder et al. 2001, and 'weighted target group'
presented in Anderson 2003). Neither approach is applicable when there are only few data (a typical case in developing countries). For example, to apply the target-group background approach to model the distribution of a bat species in North
Africa, all GBIF bat species records (Supplementary material Appendix 1, Fig. A2) are clearly not enough to serve as representative background points in this large study area. Similar to the target-group background, if the pattern of sampling bias
is known a priori, it can be used as prior weight for sampling the background proportionally to the sampling effort (e.g. 'bias file' in Maxent; Phillips and Dudík 2008, Warren et al. 2014), so that both presences and background samples have the
same bias (see also: Stolar and Nielsen 2015). As a third strategy, sampling bias can be addressed also by modelling the distribution of the focal species as a function of two additive covariate sets: the environmental covariates and other
covariate(s) describing potential sources of sampling bias, hereafter ‘bias covariates’ (model-based bias correction; Warton et al. 2013). For unbiased predictions, the bias covariates are set to a common level of bias, say 0, at all locations;
however, sometimes it is difficult to settle on a meaningful adjustment level (Warton et al. 2013). The aim of this paper is to address the problem of sampling bias in data-sparse situations and how to correct for it in presence-only SDMs. We
apply model-based bias correction, comparing two different sets of bias covariates to model the distribution of Egyptian bat species in areas of their known global distributions. Bias-models for each of three modelling techniques within the PPM
framework are calibrated with information on either accessibility or sampling effort and compared to an ‘environment-only model’. To maintain a reasonable degree of independence between training and testing datasets, we evaluated the models using
a) entirely independent presence-only data (not used to fit any of the models); and b) spatial-block cross-validation. Materials and methods Species and study area We are interested in understanding the environmental preferences of Egyptian bats
as an example representing the sampling-bias issue in data-sparse situations. We collected records for the entire range of each species (Supplementary material Appendix 1, Fig. A2, latitude: −35° to +56° and longitude: −20° to +80°) from the
literature and GBIF (see Supplementary material Appendix 2 for list of literature sources). Although GBIF provides a valuable source of data, such opportunistically compiled data bases inevitably contain misidentified or incorrectly georeferenced
records (Gaiji et al. 2013), and thus require careful revision before use. Relevant records from the GBIF database were assessed (October 2014) and merged with the available literature records. Bat records from Egypt were mostly taken from the
expert-revised BioMAP (Biodiversity Monitoring and Assessment Project) database (Basuony et al. 2010). Only species with enough presence locations that are located in at least 5 larger spatial blocks were included in this study (allowing model
evaluation on spatial-block cross-validation; see below). This was fulfilled by 21 species, each occupying > 20 unique cells at resolution of 5×5 km2 (Table 1). The geographical range of records was assessed (based on the literature and IUCN), and
spatial outliers were excluded. The coverage of all available records shows obvious signs of spatial bias towards Western Europe and only sparse sampling in Africa and Western Asia (Supplementary material Appendix 1, Fig. A2). Presence locations
were purposefully split into training and testing data, using only records from outside Egypt’s boundaries for training, thereby keeping the Egyptian presence data as entirely independent evaluation data. For sampling of background points,
however, Egypt was not excluded from the study area, and hence background points can be sampled from Egypt as well (see Fig. 1 for a flowchart of the methods applied). The determination of the study area is critical, especially for presence-only
models (Pearce and Boyce 2006). We decided against a single fixed large study area that covers presence locations of all 21 species to keep only areas of potential accessibility to the bats (Barve et al. 2011) and avoid inflating the
discrimination ability of the model (e.g. higher AUC; Barve et al. 2011). Instead, for each species, the study area was determined based on the geographical extent of the records: a rectangular bounding box containing a 1000 km buffer around the
species extent of occurrence (see Supplementary material Appendix 1, Fig. A3 for an example). We used a buffer of 1000 km, as we found it suitable for the study species ‘bats’, which have, on average, high dispersal ability and large home range.
Potential covariates (and species presences) were projected into Mollweide equal-area projection and rasterised to a resolution of 5 × 5 km2. We assessed potential environmental variables for multi-collinearity, and assembled a final list of
covariates with a maximum Generalized Variance Inflation Factor value less than 3 (for details see Supplementary material Appendix 3 & Supplementary material Appendix 1, Fig. A4). Block cross-validation Cross-validation is commonly used for
evaluating model performance when no independent data are available. Random splitting does not guarantee spatial independence due to spatial autocorrelation (both training and testing data will be spatially adjacent), and so may overestimate model
performance (Bahn and McGill 2013, Radosavljevic and Anderson 2014). To maintain independence between folds and improve transferability of models, a spatial form of cross-validation was used by splitting the study area into coarse checkerboard
blocks, and then distribute blocks randomly into folds (Fithian et al. 2015). We performed 5-fold spatial-block cross-validation (hereafter: cross-validation). The larger the block size, the higher is the need for more data to be able to run
models on spatial-block cross-validation. We used blocks of 100 × 100 km2 (20 × 20 cells), which is not very strong, as we find this more appropriate for the available data. Presence and background locations within each block were used together
for model training or testing: for the three modelling algorithms, potential background locations of the left-out cross-validation fold were not used (masked) during model calibration and were used exclusively for evaluation (similar to 'masked
geographically structured approach' of Radosavljevic and Anderson 2014, see also Fig. 7 in Fithian et al. 2015). For each species, we used a different blocking structure, balancing the number of available presences between folds and avoiding
extrapolation in environmental space (for more details see Supplementary material Appendix 4). Sampling-bias models We compared models without bias correction (environment-only model, our reference) with two methods of addressing bias. Firstly, we
considered human accessibility as the main source of sampling bias and ran SDMs with additional bias covariates describing distances to nearest cities, roads and protected areas (the ‘accessibility model’). For bias-free predictions, we set all
distances to zero; thus, a bias-free prediction can be interpreted as the relative intensity of the target species records if all locations across the study area had perfect accessibility (Warton et al. 2013). Second, assuming relative effort is
the main source of sampling bias, we incorporated a single bias covariate describing the relative intensity of sightings of all bat species (the ‘effort model’). This sampling-effort bias covariate was actually the prediction from a (different)
all-bats-model, which predicted the number of all records as a function of non-environmental variables (terrain roughness, distance to cities, distance to main roads, human population density, protected area – details in Supplementary material
Appendix 5 and Fig. 1 bottom-right). For bias-adjusted predictions, the sampling-effort covariate needed to be set to a common level, for which there is no obvious choice. We therefore adjusted it to either of two values of sampling effort: the
maximum fitted value at the target species' training presence locations, and at zero. In the first case, the bias-adjusted prediction can be interpreted as the relative intensity of species reporting if all the study area receives the sampling
effort of the best presence location of the target species. In the second case, the bias-adjusted prediction is independent of effort, and the effort covariate is used only to correct the coefficients of the environmental variables. Although the
latter value seems simpler, the predicted values lack intuitive interpretation. As the results were very similar, we here only use the maximum fitted value at training presences. Modelling algorithms For each sampling bias model (environment-only,
accessibility and effort), we employed three modelling algorithms under the PPM framework with cross-validation and adjustment for model complexity: GLM, elastic net, and Maxent. Both GLM and elastic net model the number of records as a Poisson
regression, with elastic net including a mixture of lasso and ridge regularisation (shrinkage; L1- and L2-regularisation, respectively; Friedman et al. 2010). Maxent (v3.3.3k; Phillips and Dudík 2008) is a machine-learning algorithm for
presence-only data, effectively and mathematically akin to a Poisson GLM, but with different functional forms for the predictors; it also applies an ad-hoc form of lasso regularisation (Renner and Warton 2013). We used GLM and elastic net to
implement a “down-weighted Poisson regression” (DWPR, following Renner et al. 2015). This approach uses weights to make the number of presences a negligible proportion of all data and scales the data to the actual area. As a consequence, DWPR
estimates model parameters including the intercept. A small weight (10-6) was assigned to presence locations, while background points were given a higher weight equal to the area of the study region divided by the number of background points used.
To estimate the appropriate number of background points (for GLM and elastic net), 25 repeated series of DWPR-GLMs were run, each one progressively increasing the number of randomly sampled background points. We used the number of background
points at which the log-likelihood asymptoted (Supplementary material Appendix 1, Fig. A5; Renner et al. 2015). For both GLM and elastic-net models, 1) we included linear, quadratic and 1st-order interactions between variables; 2) no interactions
were allowed between the environmental and bias covariates (Warton et al. 2013); 3) we standardised all covariates to a mean of zero and standard deviation of one. For GLMs, a random sample of background points (number estimated from the
asymptoted log-likelihood curve) was used to run an initial model. The initial model was then simplified using AIC-informed backward stepwise selection and the remaining variables were used to cross-validate the final models. Running elastic net
(R package glmnet; Friedman et al. 2010) requires tuning of two parameters, α (describes the balance of ridge and lasso) and λ (degree of regularisation; for more details see: Hastie et al. 2009). For each species and bias manipulation, we
estimated the best combination of α and λ by 5-fold cross-validation of 11 models (α ranging from zero to one with an increment of 0.1). For each model, the optimal λ value was determined by fitting a series of cross-validated models to a range of
λ values (‘regularisation path’; by default 100 values estimated from the data) and the λ value that showed the minimum mean cross-validated error was used for predictions. Similarly, the α value with the lowest error (Poisson deviance) was
selected (Supplementary material Appendix 1, Fig. A6). To report the performance of the elastic net (and for comparisons with the results of other techniques), the selected values of α and λ were used to run the cross-validation models manually.
Due to the computational limitation of explicitly using a user-defined λ during model training (stated by glmnet help page), models were fitted without providing a λ-value, allowing the fit of many models over the regularisation path. For
prediction we used the optimal λ-value estimated from cross-validation. The best-estimated values of α are shown in Supplementary material Appendix 1, Table A2. Lasso (α = 1) rather than ridge was chosen for almost half of the species in
environment-only and accessibility models. For the effort model, only three species had ridge models (α = 0) and all others had α-values 1. Maxent default settings were adapted according to advice in the literature (Merow et al. 2013,
Radosavljevic and Anderson 2014). Maxent, by default, uses combinations of feature classes (transformations of covariates: linear “L”, quadratic “Q”, hinge “H”, threshold “T”, and product “P”) depending on the number of presence locations
available, allowing for complex species-environment relationships (Phillips and Dudík 2008). We adapted functions from the ENMeval package (Muscarella et al. 2014) to run Maxent models on cross-validation at different complexity levels and feature
class combinations (48 models = 8 regularisation multiplier values ranging from 0.5 to 4 with increment of 0.5 × 6 feature class combinations [L / LQ / H / LQH / LQHP / LQHPT]). The default number of background points used by Maxent (10,000) is
insufficient to represent the environmental variability in large study areas as used here (Renner and Warton 2013), and hence all potential grids were considered as background points. We used clamping while predicting to the left-out fold, meaning
that if any value of a covariate is beyond its training range, these values will be replaced by the closest value during training (Anderson and Raza 2010). For each species and bias manipulation, the combination of regularisation multiplier and
feature class that shows the highest mean testing-AUC (on cross-validation) were selected for predictions. The optimum combinations of Maxent’s feature classes and regularisation multiplier are shown in Supplementary material Appendix 1, Table A1.
The selected feature classes deviated from Maxent’s default: 10 species always had simple features (L/LQ) for all bias manipulations, with the effort model showing more complex features in some cases. Moreover, the best-estimated regularisation
multiplier also deviated from the default value of one, with many species having values >1, indicating little overfitting. Model evaluation We evaluated the models using threshold-independent (the area under the ROC curve, AUC) and
threshold-dependent (True Skill Statistic, TSS) metrics. We tried to avoid some of the metrics' known caveats through 1) the use of species-specific study areas; 2) block cross-validation minimising environmental extrapolation; and 3) using the
same blocking structure to run different modelling techniques and bias manipulations of the same species. In presence-only SDMs, presences comprise only a tiny fraction of the background. During evaluation, the use of too many background points
with equal weights for commission and omission error can distort the evaluation (Lobo et al. 2008). To be able to compare AUCs (computed using the dismo R package) among models for the same species, we set the numbers of test presences and random
test background (test data prevalence) to a ratio of 1:20, and repeated this 100 times to average stochastic effects. TSS was calculated using the threshold that maximises the sum of sensitivity and specificity (Liu et al. 2013), again using a
constant ratio of presences and background. AUC and TSS were calculated for each combination of species, algorithm and bias manipulation. We summarised the overall effect of different bias manipulations in two ways, using linear mixed-effect
models (R-package lme4; Bates et al. 2015). Firstly, to evaluate the effect of incorporating bias covariates into the model, we compared evaluation of the environment-only models (without any bias correction) to those of bias-accounted models
(accessibility and effort) without conditioning on a particular value of the bias covariate during prediction (modelling evaluation). Second, to explore the effect of bias correction on model evaluation, we performed similar comparisons, with
bias-free predictions of the bias-accounted models instead (bias correction evaluation; for details see Supplementary material Appendix 6). We expect models incorporating the impact of bias to outperform (signified by a higher AUC or TSS) those
that do not. The problem is that we do not have bias-free data, and therefore our test data exhibit the same bias as the data used to create the model. Under these circumstances, models allowing for bias may be worse than those that do not. In
either case, the difference between bias-corrected and control models is a measure of the impact of bias. In the mixed models, we used model evaluation as response variable, species as random effect, and model type, bias correction (and their
interactions), total number of training presences, and total number of pixels at per-species study area (range size) as fixed effects (for more details, see Supplementary material Appendix 6). Results Validation by block cross-validation vs. by
Egypt hold-out The overall mean AUC is 0.88 ± 0.08 on cross-validation (0.75 ± 0.13 in Egypt’s evaluation; Figs. 2-3). Because results for AUC and TSS were similar, we present only results for AUC (see Supplementary material Appendix 1, Fig. A11
and supplement for TSS). Model evaluations in Egypt were, on average, poorer than on cross-validation. However, both types of evaluation (using ‘bias-corrected’ predictions) show positive correlation (Kendall’s tau; n=21 – Supplementary material
Appendix 1, Fig. A7), with highest consistency for the accessibility model. As expected, species with fewer occupied cells tend to have higher evaluation variability (uncertainty), and hence provide less robust analyses (Supplementary material
Appendix 1, Figs. A9-10). Effect of bias corrections: mixed-effect model analysis across species and model types Sampling-bias model explained most of the variation in model validation, followed by the modelling algorithm, and their interaction
(Fig. 2 and Supplementary material Appendix 6.1). The total number of training presence (positive effect) and the range size (negative effect) were much less important. On average, the accessibility model performed much better than
environment-only and effort models (Figs. 2 and Supplementary material Appendix 6.1). For mean cross-validations, effort models also had relatively higher AUCs than the environment-only model (the difference is much smaller for elastic net and
GLM; Figs. 2a). However, for validation in Egypt, effort models were similar to the environment-only model (Figs. 2b , see also Supplementary material Appendix 6.1). We can also evaluate the performance of the sampling-bias models when their bias
covariates are set to a fixed value, i.e. when predicting to bias-free data. However, since we have no reference survey data to compare them to, these predictions reveal the impact of bias-correction on the model, rather than assess the model’s
performance. These evaluations are presented in Fig. 3 and Supplementary material Appendix 6.2. Effect of model type The predictive performance of the three modelling algorithms showed fair to moderately high correlation coefficient (most r > 0.6,
all significant; Fig. 4). For mean cross-validation evaluations, GLM performed best, followed by elastic net and Maxent. The order is reversed for independent validations in Egypt: Maxent has highest AUC-values, followed by elastic net, then GLM
(Figs. 2-4, and Supplementary material Appendix 6). Discussion Sampling bias, if not corrected for effectively, can substantially affect the predicted intensity and model evaluation of SDMs. Our results suggest that accessibility bias covariates
describe the bias in our focal species’ training data well, compared to sampling efforts, and their use led to higher validation scores. Evaluated on data that are themselves spatially biased, we find that removing sampling bias did not improve
the predictive performance on cross-validation or in Egypt (Fig. 3), highlighting the limitation of evaluating bias correction without independent bias-free presence-absence data. Collectively, the three modelling algorithms performed similarly
well in cross-validation, though predicting to new sites (Egypt) gave Maxent a slight advantage (Figs. 2b and 3b). Sampling-bias correction using presence-only data Few approaches exist to correct for sampling bias, some not applicable when data
are sparse. Spatial filtering (i.e. aggregation to single records within some larger buffer: e.g. Anderson and Raza 2010, Boria et al. 2014) might be wasteful when only few presences exist. Removal of clumped data will reduce training sample size
and may remove some of the environmental conditions occupied by the species (depending on the heterogeneity of the landscape, selected distance, and pixel size). Target-group background selection strictly assumes that related species were
collected with the same method and equipment (Phillips et al. 2009), bias is similar across species (Warton et al. 2013), and species have the same chance of being recorded in all locations (Yackulic et al. 2013). Moreover, it replaces the
observer bias with a (spatial) species-richness bias and can be understood as modelling the likelihood of encountering the target species rather than a non-target species (Warton et al. 2013, Warren et al. 2014). Also, it does not distinguish
between areas unsuitable for any of the species and areas of low accessibility (no records, but potentially suitable: Warren et al. 2014, Fithian et al. 2015). The target-group background cannot be used when data on the related species are
similarly limited, as this increases the risk of extrapolating in environmental space (Mateo et al. 2010, Merow et al. 2013). Bias layers attempt to describe with which biases presence locations were recorded (Phillips et al. 2009, Warton et al.
2013). Our external sampling-effort model (Fig. 1 bottom right) is such an attempt to derive a bias layer (e.g. Elith et al. 2010). The bias layer is currently only implemented in Maxent, and we are not aware of any study that applied a similar
approach using other modeling algorithms. To maintain consistency of the analyses across different modelling algorithms we did not consider using a bias layer here. Both bias layer and target-group are used to sample background with the same bias
as presence locations, which is a sensitive tuning step that strongly influences model evaluation (Chefaoui and Lobo 2008). We think that model-based bias correction, as applied here, is more plausible in data deficient situations and if applied
efficiently, it frees us from artificially manipulating presences or background points, and rather focus on sampling bias correction. The effectiveness of bias correction depends on whether bias covariates are actually able to describe the bias in
the available data. Our use of either accessibility or sampling effort bias covariates did not lead to notably different conclusions (see Fig. 5). Using sampling-effort bias covariate led to, on average, little to moderate evaluation changes
(Figs. 2-3). It is in fact a model-based version of the target-group background approach, without strict selection of the background data points. The assumption that closely related species have similar bias may not hold. Surprisingly, most of the
available presences of our focal species were located in areas of low to moderate estimated efforts (Supplementary material Appendix 1, Fig. A13), but still strongly biased towards roads and cities (and, to less extent, protected areas;
Supplementary material Appendix 1, Fig. A13). Ideally, evaluating bias correction requires independent ‘bias-free’ presence-absence testing data (Phillips et al. 2009). Such data are typically not available, especially in developing countries, and
removing bias from test data is very difficult (Dudík et al. 2005, Smith 2013). On average, validation of bias-corrected predictions using well-structured, independent presence-absence data from rigorous surveys led to improved predictions (Elith
and Leathwick 2007, Phillips et al. 2009, Mateo et al. 2010, Syfert et al. 2013, Warton et al. 2013, Boria et al. 2014). However, this improvement is not happening in all situations and depends on the modelling conditions, species prevalence,
validity of assumptions, and how effective bias covariates are in describing bias in training presences (Phillips et al. 2009, Warton et al. 2013, Fourcade et al. 2014). As covariates that affect sampling may also affect the distribution of a
species (e.g. avoiding deserts), no method can fully correct for sampling bias in presence-only data without affecting the niche model (Merow et al. 2014, Guillera-Arroita et al. 2015). Correction of sampling bias leads to larger areas of suitable
habitats due to higher suitability estimates in low-accessible sites (e.g. Phillips et al. 2009, Warton et al. 2013; Fig. 5). Predictions at such sites are of lower reliability and should be interpreted with caution (Supplementary material
Appendix 1, Fig. A16 for an example). They can be used to guide future surveys and conservation planning, but not for taking serious conservation decisions (Guisan et al. 2006). Evaluations using spatial-block cross-validation vs. Egyptian
hold-out We used spatial-block cross-validation to avoid overestimating model performance and underestimating predictive errors (Bahn and McGill 2013, Renner et al. 2015, Roberts et al. 2017). Block cross-valuations suggested a better model
performance than evaluation on Egyptian data. This can be explained by differences in sample size and by environmental variability: on average, our cross-validation models had a larger mean number of testing presences and higher environmental
variability compared to evaluations at smaller scale (Table 1). However, evaluations at both scales were positively correlated, which supports the idea that evaluations on cross-validation (larger extent) can be indicative of performance at the
local scale. Evaluation metrics & predictive performance Using AUC and TSS led to consistent conclusions. The overall evaluation scores are fair to high, taking into account that spatially independent evaluation yields lower scores compared to
commonly used random split (Radosavljevic and Anderson 2014). In presence-only SDMs, the use of a particular value for defining good models become unreliable (Yackulic et al. 2013), due to higher uncertainty of estimates at background points and
as the number of background points used is not fixed. In this study, we maintained constant test-data prevalence (1:20) across all comparisons, which gave very similar results, across all species, to the standard default approach of computing AUC
(see Supplementary material Appendix 1, Fig. A14). For some species, the spread over the 100 repetitions was very noticeable, however, making our approach somewhat more robust. The improved predictive performance reported by Syfert et al. (2013),
for example, may be in part attributable to much higher testing prevalence. Also in our study, the larger the number of available presences and the smaller the study area was, the higher were the predictions scores. Comparison of modelling
algorithms The three modelling algorithms applied did not lead to different conclusions and their evaluations were highly correlated. Elastic-net models showed intermediate performance in all situations. GLM (more specifically: the down-weighted
Poisson regression (DWPR) with variable selection) had the highest evaluation on cross-validation, which may suggest that GLM-DWPR is more powerful with a larger number of testing presences. However, GLMs predictions in Egypt were less nuanced
compared to other two modelling algorithms (Supplementary material Appendix 1, Fig. A15a, for example), which explains why it ranked lowest on the Egyptian hold-out. Maxent had the lowest prediction error on the Egyptian data, which suggests its
transferability to situations of low extrapolation. However, Maxent had the lowest evaluation on cross-validation, possibly due to clamping. We applied ‘clamping’ to constrain the response beyond the training range, which changes some of the
predicted values. Clamping can affect model evaluation (the ranking of the predicted values) and, while its effect has not been well-explored in the literature, it seems to depend on the shape of the response curve (at both ends), the importance
of the covariate, and how much environmental extrapolation occurs. We expect the effect of clamping to be small in the Egyptian hold-out compared to the cross-validation, due to less extrapolation. When correcting for bias, no interaction should
be allowed between bias and other covariates so that, for prediction, the bias can be corrected for without affecting the other covariates (Warton et al. 2013). For GLM and elastic net, we have full control of the models’ interactions. However,
the version of Maxent used here (3.3.3k) does not enable users to select which interactions to use, and the use of the product feature inevitably enables all pairwise interactions. In further applications, it may be recommended to disable the
‘product’ feature class while correcting for sampling bias. However, its use here did not lead to different conclusions compared to GLM and elastic net, suggesting that bias-suitability interactions were of limited importance. During the reviewing
of this manuscript, an open-source version of Maxent (maxnet R package: Phillips et al. 2017) was released that uses the glmnet package for L1-regularization. Maxnet provides flexibility for specifying the interactions to be used, so it is
possible to exclude interactions between environmental and bias variables (making them similar to our elastic-net models, but with more flexibility for other feature classes implemented in Maxent, e.g. the hinge). This early version of maxnet
implements an Infinitely-Weighted Logistic Regression (IWLR; Fithian and Hastie 2013) and only L1-regularization (lasso); however, further extensions are possible, e.g. the implementation of DWPR and elastic net (similar to our elastic-net
models). We implemented the down-weighted Poisson regression using both GLM and elastic net. As Poisson models, their predictions have no upper bound and may thus yield extreme predictions. We reported the existence of a few extreme predicted
intensities for many species, which makes it difficult to plot their predictions on a linear scale (see Fig. 5 and Supplementary material Appendix 1, Fig. A15b for an example). In contrast, Maxent puts a constraint on the moments of the
predictions, making them less subject to extreme values (Phillips et al. 2006). Conclusion Data-sparse regions pose challenges to modelling species distributions, exacerbated by noticeable sampling biases. We recommend the use of model-based bias
correction in data-sparse situations, in which other bias corrections methods are not possible; however, the effectiveness of bias correction depends on whether bias covariates are actually able to describe the bias in the available data. Using
covariates to describe site accessibility improved prediction to spatially independent hold-outs, compared to environment-only or effort models. Augmenting local records with data from across the species’ range allowed us to make consistently
high-quality predictions to hold-out data from an entire country (in this case Egypt). Bias-free predictions can enhance future conservation planning and target future surveys when limited resources are available to cover large study areas.
However, due to possible lower certainty at unsurveyed locations, they should be used cautiously (maps including bias are of use only during model cross-validation). Without survey-based presence-absence data, no complete evaluation of the quality
of bias corrections can be attempted. Down-weighted Poisson regression as well as the statistically equivalent Maxent approach led to similar results, with more flexibility in the elastic-net models (e.g. degree of shrinkage, question-led
specification of non-linear effects and interactions). More important than the specific algorithm is to use the point-process modelling framework as such. Acknowledgements We would like to express our sincere thanks for Petr Benda (Charles
University) for comments on the distribution of the bat species. An earlier version of the manuscript was improved by comments of Prof. Francis Gilbert (University of Nottingham). We are also grateful to Belarmain Fandohan, David R. Roberts, and
Simone Ciuti for long discussions and comments on the manuscript. This manuscript benefitted from comments of the subject editor Robert P. Anderson and two anonymous reviewers. A. El-G. is sponsored by the German Academic Exchange Service (DAAD)
through a GERLS scholarship. This work was partially performed on the computational resource ‘bwUniCluster’ funded by the Ministry of Science, Research and Arts and the Universities of the State of Baden-Württemberg, Germany, within the framework
program bwHPC. References Anderson, R. P. 2003. Real vs. artefactual absences in species distributions: Tests for Oryzomys albigularis (Rodentia: Muridae) in Venezuela. – Journal of Biogeography 30: 591–605. Anderson, R. P. and Raza, A. 2010. The
effect of the extent of the study region on GIS models of species geographic distributions and estimates of niche evolution: preliminary tests with montane rodents (genus Nephelomys) in Venezuela. – J Biogeogr 37: 1378–1393. Bahn, V. and McGill,
B. J. 2013. Testing the predictive performance of distribution models. – Oikos 122: 321–331. Barve, N. et al. 2011. The crucial role of the accessible area in ecological niche modeling and species distribution modeling. – Ecol Model 222:
1810–1819. Basuony, M. I. et al. 2010. Mammals of Egypt: atlas, red data listing & conservation. BioMAP & CultNat, EEAA & Bibliotheca Alexandrina, Cairo. 286 pp. Bates, D. et al. 2015. Fitting Linear Mixed-Effects Models Using lme4. – J Stat Softw
67. Boria, R. A. et al. 2014. Spatial filtering to reduce sampling bias can improve the performance of ecological niche models. – Ecol Model 275: 73–77. Chefaoui, R. M. and Lobo, J. M. 2008. Assessing the effects of pseudo-absences on predictive
distribution model performance. – Ecol Model 210: 478–486. Dudík, M. et al. 2005. Correcting sample selection bias in maximum entropy density estimation. Advances in Neural Information Processing Systems 18. The MIT Press, pp. 323-330. URL:
http://papers.nips.cc/paper/2929-correcting-sample-selection-bias-in-maximum-entropy-density-estimation.pdf. Elith, J. et al. 2010. The art of modelling range-shifting species. – Methods Ecol Evol 1: 330–342. Elith, J. et al. 2011. A statistical
explanation of MaxEnt for ecologists. – Divers Distrib 17: 43–57. Elith, J. and Leathwick, J. 2007. Predicting species distributions from museum and herbarium records using multiresponse models fitted with multivariate adaptive regression splines.
– Divers Distrib 13: 265–275. Fithian, W. et al. 2015. Bias correction in species distribution models: pooling survey and collection data for multiple species. – Methods Ecol Evol 6: 424–438. Fithian, W. and Hastie, T. 2013. Finite-sample
equivalence in statistical models for presence-only data. – Ann Appl Stat 7: 1917–1939. Fourcade, Y. et al. 2014. Mapping species distributions with MAXENT using a geographically biased sample of presence data: a performance assessment of methods
for correcting sampling bias. – PloS one 9: e97122. Friedman, J. H. et al. 2010. Regularization paths for generalized linear models via coordinate descent. – Journal of statistical Software 33 - http://www.jstatsoft.org/v33/i01/paper. Gaiji, S. et
al. 2013. Content assessment of the primary biodiversity data published through GBIF network: status, challenges and potentials. – Biodiversity Informatics 8: 94–122. Guillera-Arroita, G. et al. 2015. Is my species distribution model fit for
purpose? Matching data and models to applications. – Global Ecol Biogeogr 24: 276–292. Guisan, A. et al. 2006. Using Niche-Based Models to Improve the Sampling of Rare Species. – Conservation Biology 20: 501–511. Hastie, T. et al. 2009. The
elements of statistical learning: data mining, inference, and prediction - Springer New York. Liu, C. et al. 2013. Selecting thresholds for the prediction of species occurrence with presence-only data. – J Biogeogr 40: 778–789. Lobo, J. M. et al.
2008. AUC: a misleading measure of the performance of predictive distribution models. – Global Ecol Biogeogr 17: 145–151. Mateo, R. G. et al. 2010. Profile or group discriminative techniques? Generating reliable species distribution models using
pseudo-absences and target-group absences from natural history collections. – Divers Distrib 16: 84–94. Merow, C. et al. 2013. A practical guide to MaxEnt for modeling species’ distributions: what it does, and why inputs and settings matter. –
Ecography 36: 1058–1069. Merow, C. et al. 2014. What do we gain from simplicity versus complexity in species distribution models? – Ecography 37: 1267–1281. Muscarella, R. et al. 2014. ENMeval: an R package for conducting spatially independent
evaluations and estimating optimal model complexity for Maxent ecological niche models. – Methods Ecol Evol 5: 1198–1205. Newbold, T. 2010. Applications and limitations of museum data for conservation and ecology, with particular attention to
species distribution models. – Progress in Physical Geography 34: 3–22. Pearce, J. L. and Boyce, M. S. 2006. Modelling distribution and abundance with presence-only data. – J Appl Ecol 43: 405–412. Phillips, S. J. et al. 2006. Maximum entropy
modeling of species geographic distributions. – Ecol Model 190: 231–259. Phillips, S. J. et al. 2009. Sample selection bias and presence-only distribution models: implications for background and pseudo-absence data. – Ecological Applications 19:
181–197. Phillips, S. J. et al. 2017. Opening the black box: an open-source release of Maxent. – Ecography. Phillips, S. J. and Dudík, M. 2008. Modeling of species distributions with Maxent: new extensions and a comprehensive evaluation. –
Ecography 31: 161–175. Ponder, W. F. et al. 2001. Evaluation of Museum Collection Data for Use in Biodiversity Assessment. – Conservation Biology 15: 648–657. Radosavljevic, A. and Anderson, R. P. 2014. Making better Maxent models of species
distributions: complexity, overfitting and evaluation. – J. Biogeogr. 41: 629–643. Renner, I. W. et al. 2015. Point process models for presence-only analysis. – Methods Ecol Evol 6: 366–379. Renner, I. W. and Warton, D. I. 2013. Equivalence of
MAXENT and Poisson point process models for species distribution modeling in ecology. – Biometrics 69: 274–281. Roberts, D. R. et al. 2017. Cross-validation strategies for data with temporal, spatial, hierarchical, or phylogenetic structure. –
Ecography 28. Smith, A. B. 2013. On evaluating species distribution models with random background sites in place of absences when test presences disproportionately sample suitable habitat. – Diversity Distrib. 19: 867–872. Stolar, J. and Nielsen,
S. E. 2015. Accounting for spatially biased sampling effort in presence-only species distribution modelling. – Divers Distrib 21: 595–608. Syfert, M. M. et al. 2013. The effects of sampling bias and model complexity on the predictive performance
of MaxEnt species distribution models. – PloS one 8: e55158. Warren, D. L. et al. 2014. Incorporating model complexity and spatial sampling bias into ecological niche models of climate change risks faced by 90 California vertebrate species of
concern. – Divers Distrib 20: 334–343. Warton, D. and Aarts, G. 2013. Advancing our thinking in presence-only and used-available analysis. – The Journal of Animal Ecology 82: 1125–1134. Warton, D. I. et al. 2013. Model-based control of observer
bias for the analysis of presence-only data in ecology. – PloS one 8: e79168. Yackulic, C. B. et al. 2013. Presence-only modelling using MAXENT: when can we trust the inferences? – Methods Ecol Evol 4: 236–243. Table 1: List of Egyptian bat
species used in this study, with total number of records available, number of unique records (in parentheses: the number of records used to train the model on cross-validation/those kept aside for independent evaluation, i.e. ‘Egyptian records’),
number of occupied grid cells at the resolution of 5 × 5 km (number of cells outside/inside Egypt), and best estimated number of background points used to run the DWPR-GLM and elastic-net models. See main text and Supplementary material Appendix
1, Fig. A5 for more details. Species # Records (Total) # Records (unique) # occupied cells # background points (×1000) Asellia tridens (Trident Leaf-nosed Bat) Barbastella leucomelas (Sinai Barbastelle) Eptesicus bottae (Botta’s Serotine Bat)
Hypsugo ariel (Fairy Pipistrelle) Nycteris thebaica (Egyptian Slit-faced Bat) Nycticeinops schlieffeni (Schlieffen's Bat) Otonycteris hemprichii (Hemprich’s Long-eared Bat) Pipistrellus deserti (Desert Pipistrelle) Pipistrellus kuhlii (Kuhl's
Pipistrelle) Pipistrellus rueppellii (Rueppell’s Pipistrelle) Plecotus christii (Desert Long-eared Bat) Rhinolophus clivosus (Arabian Horseshoe Bat) Rhinolophus hipposideros (Lesser Horseshoe Bat) Rhinolophus mehelyi (Mehely’s Horseshoe Bat)
Rhinopoma cystops (Lesser Mouse-tailed Bat) Rhinopoma microphyllum (Greater Mouse-tailed Bat) Rousettus aegyptiacus (Egyptian Fruit Bat) Tadarida aegyptiaca (Egyptian Free-tailed Bat) Tadarida teniotis (European Free-tailed Bat) Taphozous
nudiventris (Naked-Bellied Tomb Bat) Taphozous perforatus (Tomb Bat) Figure 1: Flowchart of analyses in this study, illustrated with data for Asellia tridens. Sampling-bias models and modelling algorithms were combined factorially. Only results
for validation with AUC are presented in the manuscript, while TSS-results are given in the appendix. Figure 2: Mean AUC of each species calculated either on 5-fold spatial block cross-validation (a) or in Egypt (b). Each plot compares evaluation
of environment-only models to bias-accounting models (effort and accessibility), without correcting for sampling bias (Modelling evaluation; see Appendix 5.1). Each species is represented by different symbols (see Supplementary material Appendix
1, Fig. A7 for species names). Red lines indicate overall mean AUC for each modelling algorithm and bias manipulation applied. For evaluations of bias-free prediction, see Fig. 3. Figure 3: Species mean AUC calculated either on cross-validation
(a) or in Egypt (b), after sampling bias correction (using bias-free prediction; for details, see Supplementary material Appendix 6.2). Each species is represented by different symbols (see Supplementary material Appendix 1, Fig. A7 for species
names). Red lines indicate the overall mean AUC at each modelling algorithm and bias models applied. Figure 4: Kendall’s correlation of the per-species mean AUC between pairs of modelling algorithms. Each species is represented by different
symbols (see Supplementary material Appendix 1, Fig. A7 for species names) with colours referring to bias models (using predictions of environment-only model and bias-free prediction of accessibility and effort model). ‘M’ indicates the overall
mean evaluation. Top row panels are mean evaluation using spatial block cross-validation, while those in the bottom row are independent evaluations in Egypt. Figure 5: Mean cross-validated predicted distribution of Otonycteris hemprichii, of
different modelling algorithms (rows) and bias models (columns). Maps were rescaled to relative intensities between zero and one, as different modelling algorithms do not have the same scale. Darker colour indicates higher predicted relative
intensity. Blue points (in the top left panel) represents available records used for cross-evaluation model training. For visualisation, extreme values (> 0.9995 quantile of predicted values) were replaced with their next smaller value, as GLM and
elastic net are subject to some few extreme predictions (see main text, and Supplementary material Appendix 1, Fig A15B for a comparison with unlimited predictions). For predicted maps in Egypt see Supplementary material Appendix 1, Fig. A15A.
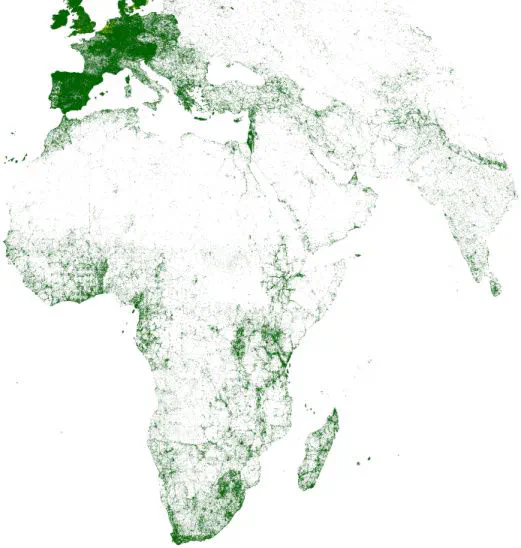 GBIF
GBIF