Fin whale (Balaenoptera physalus) distribution modeling on their Nordic and Barents Seas feeding grounds

Fin whale (Balaenoptera physalus) distribution modeling on their Nordic and Barents Seas feeding grounds Diandra Duengen, Elke Burkhardt, Ahmed El-Gabbas Ocean Acoustics Group, Alfred Wegener Institute (AWI), Helmholtz Centre for Polar and Marine Research, Bremerhaven, Germany Klußmannstraße 3d, DE-27570 Bremerhaven, Germany Understanding cetacean distribution is essential for conservation planning and decision-making, particularly in regions subject to rapid environmental changes. Nevertheless, information on their spatiotemporal distribution is commonly limited, especially from remote areas. Species distribution models (SDMs) are powerful tools, relating species occurrences to environmental variables to predict the species’ potential distribution. This study aims at using presence-only SDMs (MaxEnt) to identify suitable habitats for fin whales (Balaenoptera physalus) on their Nordic and Barents Seas feeding grounds. We used spatial-block cross-validation to tune MaxEnt parameters and evaluate model performance using spatially independent testing data. We considered spatial sampling bias correction using four methods. Important environmental variables were distance to shore and sea ice edge, variability of sea surface temperature and sea surface salinity, and depth. Suitable fin whale habitats were predicted along the west coast of Svalbard, between Svalbard and the eastern Norwegian Sea, coastal areas off Iceland and southern East Greenland, and along the Knipovich Ridge to Jan Mayen. Results support that presence-only SDMs are effective tools to predict cetacean habitat suitability, particularly in remote areas like the Arctic Ocean. SDMs constitute a cost-effective method for targeting future surveys and identifying top priority sites for conservation measures. 1. Introduction The Nordic Seas are a large part of the Arctic Ocean, comprising the Greenland-, Norwegian- and Iceland Seas (Campos & Horn, 2018; Figure. 1; Loeng & Drinkwater, 2007). The Arctic Ocean has unique physical characteristics, including strong seasonality in light, overall cold temperatures, and extensive shelf areas around a deep oceanic basin (Drange et al., 2005; Kovacs et al., 2010; Loeng & Drinkwater, 2007). During summer months, high primary production leads to seasonally abundant marine mammals that use this area as feeding grounds (Derville et al., 2019; Laidre et al., 2010; Loeng & Drinkwater, 2007), including fin whales (Balaenoptera physalus) (Heide-Jørgensen et al., 2008; Heide-Jørgensen et al., 2010; Heide-Jørgensen et al., 2007; Heide-Jørgensen et al., 2003; Joiris et al., 2014; Laidre et al., 2010; Mikkelsen et al., 2007; Nøttestad et al., 2014; Storrie et al., 2018). Figure 1: Map of the study area, covering 60°N - 81°N and 45°W - 55°E. The blue color represents depth: shallow waters (light blue), deep waters (dark blue) (source: GEBCO; Weatherall et al. 2015). The large yellow, green, and red diamonds represent Knipovich Ridge, Mohns Ridge, and Jan Ma-yen, respectively. Dots represent all fin whale sightings used in the models, with colors indicating the data source. Dark gray areas depict land. The yellow line indicates the approximate mean posi-tion of the Polar Front, as defined by Harris et al. (1998). The Arctic sea ice and sea ice extent have decreased substantially in the past decades due to climate change and most likely will continue declining in the following decades (Overland & Wang, 2013). Altered current patterns are expected to change species composition in regions such as Svalbard, e.g., due to poleward shifts of boreal generalists (e.g., fishes and euphausiids), potentially displacing native Arctic species (Carmack & Wassmann, 2006; Dalpadado et al., 2016; Fossheim et al., 2015; Gluchowska et al., 2016; Kortsch et al., 2015; Loeng & Drinkwater, 2007). These alterations are predicted to result in changes in the abundance and distribution of cetaceans in the Arctic (see Moore et al., 2019 for a review; Storrie et al., 2018; Tynan & DeMaster, 1997; Víkingsson et al., 2015). Sea ice has been one of the limiting factors restricting human access to high latitudes, but the decreasing sea ice coverage due to climate change may increase anthropogenic activities in the Arctic Ocean (such as shipping, fishing, and oil and gas exploration) (Alter et al., 2010; Burek et al., 2008; Gjøsæter et al., 2009). This could further affect cetaceans in this area, especially fin whales, which are particularly vulnerable to ship strikes (Cates et al., 2017; Laist et al., 2001; Schleimer et al., 2019) and entanglement (Ramp et al., 2021). Climate change is expected to strongly impact fin whale populations (Aguilar, 2009; Tulloch et al., 2019). Fin whales in the North Atlantic have already displayed altered temporal migration patterns in response to rising sea surface temperature and earlier ice break-up (Ramp et al., 2015), and a distributional expansion was assumed as feeding response to physical and biological changes in the Irminger Sea (Víkingsson et al., 2015). According to the most recent global IUCN Red List assessment, fin whales are listed as ‘Vulnerable’, with an increasing population trend (Cooke, 2018). Fin whales generally occur in temperate and cold waters of the world (Aguilar & García-Vernet, 2018). Fin whales generally migrate between summer feeding grounds at high latitudes and winter breeding grounds at low latitudes (Edwards et al., 2015; Mizroch et al., 2009). However, some individuals stay at high latitudes throughout winter (Edwards et al., 2015; Haver et al., 2017; Lydersen et al., 2020; Moore et al., 2012; Simon et al., 2010). They are also common in temperate waters (e.g., in the Mediterranean Sea) (Forcada et al., 1996; Gannier, 2002). Fin whales are opportunistic feeders that forage on krill and pelagic fish (Santora et al., 2010; Sigurjónsson & Víkingsson, 1997; Skern-Mauritzen et al., 2011) and likely are capable of switching prey upon availability (Gavrilchuk et al., 2014). Studies of fin whale distribution in the Nordic Seas (e.g., Nøttestad et al., 2014; Skern-Mauritzen et al., 2011; Storrie et al., 2018; Víkingsson et al., 2015) are still limited compared to other regions, such as the Mediterranean (e.g., Druon et al., 2012; Sciacca et al., 2015), but currently increasing. Species distribution models (SDMs), also known as ecological niche models, are helpful tools linking species occurrences to environmental conditions to provide insight into potential species’ distribution. Correlative SDMs estimate the relationship between species occurrences (presence-only or presence-absence) and environmental characteristics in a given study area (Franklin, 2010). SDMs for marine species are generally less frequent than for terrestrial species, yet there is a notable increase in their application in the marine realm (Robinson et al., 2011; Smith et al., 2021). SDMs are particularly useful in estimating habitat suitability in remote regions with limited access, such as the polar oceans (El-Gabbas et al., 2021a; Storrie et al., 2018). Cetaceans are highly mobile and spend a considerable amount of time underwater, which hampers accurate absence data collection (Praca et al., 2009). In such cases, species data are often available in the form of presence-only data (Elith et al., 2011), e.g., from global open-access data repositories such as the Global Biodiversity Information Facility (GBIF) and Ocean Biodiversity Information System (OBIS). Despite the valued use of presence-only SDMs to support conservation decision making in data-poor situations (El-Gabbas et al., 2020; Smith et al., 2021), these data are usually opportunistic and come without information on the group size, sampling design and efforts, which can lead to spatial, temporal, or environmental biases (El-Gabbas & Dormann, 2018a; Fourcade et al., 2013). This sampling bias can highly affect SDMs performance and inference and thus needs to be corrected for (El-Gabbas & Dormann, 2018a; Phillips et al., 2009; Warton et al., 2013). A few presence-only SDM methods exist (Renner et al., 2015), amongst which is MaxEnt (Phillips et al., 2006). In addition to presence locations, MaxEnt uses a random sample of locations (background information) to characterize the environmental conditions in the study area (Phillips et al., 2006; Renner et al., 2015). Detailed information on how MaxEnt works is presented in Elith et al. (2011) and Merow et al. (2013). This study aims at using MaxEnt and presence-only sightings to identify suitable habitats for fin whales in the Nordic and Barents Seas during the feeding season (May to September) and determine important environmental variables affecting their distribution. As available sightings are opportunistic and show spatial biases, we implemented four methods to correct for sampling bias. We tuned MaxEnt parameters and evaluated model performance using spatial-block cross-validation, maintaining spatial independence between training and testing data sets. Few studies have modeled cetaceans’ potential distribution from polar regions (e.g., Bombosch et al., 2014; El-Gabbas et al., 2021b; Storrie et al., 2018; Zerbini et al., 2016), and this study is one of the first to use MaxEnt to model suitable habitats of fin whales in the Arctic Ocean. 2. Methods 2.1. Study area The study area encompasses the Nordic Seas, the Barents Sea, and northern parts of the Irminger Sea (60°N - 81°N and 45°W - 55°E; Figure 1). The boundaries of the study area were determined by inspecting fin whale data availability, with a buffering area of 20 km around sightings. Models were calibrated at an equal-area projection, following Elith et al. (2011) and Budic et al. (2016). We used a grid cell of 100 km2 (10×10 km; 51,595 cells in total) as we found this resolution a suitable compromise for the large study area, high mobility of fin whales, and the variant spatial resolution of the original environmental data (Table 1). Appropriate map projection was determined using the projection wizard tool v1.2 (Savric et al., 2016; https://projectionwizard.org/): Polar Lambert azimuthal equal-area projection (WGS 1984: EPSG 8326, with a central meridian of 5º 0' E). We excluded the Baltic Sea area from the analysis because this area is ecologically highly dissimilar to the rest of the study area, and fin whales are not commonly recorded within this area (Skóra, 1997). 2.2. Fin whale sightings Fin whale presence-only sightings from 2004 to July 2021 were collected from 18 RV Polarstern cruises (Burkhardt, 2019, for more information, see Table S1 in the Supporting Information), GBIF (https://gbif.org, accessed on July 12, 2021 via the rgbif R-Package (Geffert & Ram, 2021)), iOBIS (https://obis.org/, accessed on July 12, 2021 via the robis R-package (Provoost & Bosch, 2019)), and two relatively recent publications (Løviknes, 2019; Nøttestad et al., 2014). The total year span (2004–2021) was determined according to the availability of the data. These sightings are mainly opportunistic citizen science observations made on research cruises, whale watching boats, or from near the shore. We included only sightings from May to September, as this time frame covers fin whales’ main feeding season in the Arctic (Víkingsson, 1997). RV Polarstern data were collected from multidisciplinary research cruises to the Arctic from 2007 to 2018, with species identification conducted by nautical officers on duty, and sighting date, time, location, and group size were recorded systematically using ‘WALOG’ software v1.3 (Burkhardt, 2019). Species were identified to the lowest taxonomic level possible, associated with a certainty level of identification. Uncertain identifications (category ‘possible’) were left out of the analysis. All data were quality-controlled to exclude doubtful or erroneous occurrences (e.g., inaccurate coordinates that indicate being on land) and occurrences outside of the study area. Group size per detection was not systematically reported in available data sources. As our main objective is to estimate fin whale habitat suitability, instead of abundance, we considered each detection event as a single occurrence, irrespective of how many individuals were recorded per detection. In total, there are 1,736 independent sightings (Figures 1 and S1 in the Supporting Information). 2.3. Environmental data Our models employed static SDMs, in which species sightings were spatially matched with environmental variables summarizing environmental conditions in the Nordic and Barents Seas between 2004 and 2018, only from May to September (El-Gabbas et al., 2021b). Potential environmental variables were determined based on ecological relevance for fin whales and availability, including dynamic and static variables )see Table 1 for more information on the original spatiotemporal resolution and sources of the environmental variables). Dynamic variables include chlorophyll-a concentration, temperature and salinity at the surface (0 m) and 100 m depth, sea ice concentration, current speed, and sea surface height. Table 1: Unit, statistic, time frame, spatiotemporal resolution, and source of the 14 environmental variables used for modeling. Covariate Abbreviation Unit Statistic Spatial resolution Temporal resolution Source Depth Depth m 30 arcsecond Static GEBCO a Aspect Aspect ° 30 arcsecond Static Derived from depth Slope Slope ° 30 arcsecond Static Derived from depth Distance to shore Dist2Shore km 30 arcsecond Static Derived from depth Distance to 500 m isobath Dist2Isobath km 30 arcsecond Static Derived from depth Sea surface height SSH_SD m sd 0.25° Daily (2004-2018) COPERNICUS b Current speed Speed_mean m s-1 mean 0.25° Daily (2004-2018) COPERNICUS b Sea ice concentration SIC_mean % mean 6.25 km Daily (2004-2018) Spreen et al. (2008) Distance to sea ice edge Dist2Ice km 6.25 km Daily (2004-2018) Derived from SIC_mean Salinity (0, 100 m) Sal_100_mean, Sal_0m_SD unitless mean sd 0.25° Monthly c World Ocean Atlas 2018 Temperature (0, 100 m) Temp_0m_SD, Temp_100m_SD °C sd sd 0.25° Monthly c World Ocean Atlas 2018 Chlorophyll-a Chla_SD mg m-3 sd 4 km 8-day composite (2004–2018) OCCCI d a GEBCO: General Bathymetric Chart of the Oceans (https://www.gebco.net/; Weatherall et al. 2015). b COPERNICUS: the European Union’s Earth observation programme (https://www.copernicus.eu/). The product used: Global ocean gridded l4 sea surface heights and derived variables reprocessed (SEALEVEL_GLO_PHY_L4_REP_OBSERVATIONS_008_047). c salinity (Zweng et al. 2018) and temperature (Locarnini et al. 2018) data were available from the World Ocean Atlas at coarse temporal resolution: single monthly mean map capturing the period 2005-2017 (https://www.ncei.noaa.gov/products/world-ocean-atlas). d OCCCI: the ESA Ocean Colour Climate Change Initiative (https://www.esa-oceancolour-cci.org/; Sathyendranath et al. 2018) . We prepared two summary maps for each dynamic predictor: the mean and standard deviation of environmental conditions over five months (May-September) for each predictor-specific temporal availability range (Table 1). When used in combination with the mean, variables representing long-term environmental variability (standard deviation) can express extreme values not represented in the mean (Zimmermann et al., 2009). This can further reduce the potential effect of temporal mismatch between sightings and long-term mean environmental conditions (El-Gabbas et al., 2021b). To avoid the influence of uncertain values of sea ice concentration close to land (due to land-spillover), mean sea ice concentration values at a two cell buffer from shore were replaced with their interpolated values (Markus & Cavalieri, 2009), using “Kriging” tool in ArcGIS (ESRI, 2019, ArcMap v10.6.1). As an additional predictor, we calculated the minimum distance between each cell and the sea ice edge. We determined the sea ice edge as the largest polygon with >15% mean sea ice concentration (Parkinson, 2017; May-September). Cells intersecting with the sea ice edge line were assigned a value of zero, while cells with sea ice concentration <15% (south of the sea ice edge) were assigned positive values, and cells with sea ice concentration >15% (north of the sea ice edge) were assigned negative values (following Williams et al., 2014, see Figure S2). Static variables include depth, aspect, slope, distance to shore, and distance to 100 m, 200 m, and 500 m isobaths, all derived from the depth map (Weatherall et al., 2015). Distance to isobaths and shore were calculated using “Contour” and “Near” tools in ArcGIS. In total, 24 initial variables were prepared at consistent projection (WGS 1984: EPSG 8326, with a central meridian of 5º 0' E), extent, and resolution using ArcGIS (ESRI, 2019), QGIS (QGIS, 2019, v3.4.5), and R (R Core Team, 2019, v3.5.3). Variables were projected using spTransform function of sp R-package (Bivand et al., 2013; Pebesma & Bivand, 2005). Cells with missing values were interpolated using “Kriging” tool in ArcGIS. To maximize variables’ uniformity, potential variable transformations were checked using box-cox transformations (Box & Cox, 1964), following Dormann and Kaschner (2010), see Table S2. Multicollinearity can cause instability in parameter estimation and affect model predictions (Dormann et al., 2013; Graham, 2003). Therefore, we only considered low-correlated variables in the models: maintaining a variance inflation factor (VIF) <4, followed by ensuring a maximum Pearson correlation coefficient of 0.7 (Dormann et al., 2013; Zuur et al., 2010, see Table S2). In total, ten variables were excluded from fitting the model due to multicollinearity, which resulted in 14 variables used in the models (Table 1 and Figure S2). 2.4. Species distribution models Static models were fit using MaxEnt v3.4.1 (Phillips et al., 2017; Phillips et al., 2006) through maxent function of dismo R-package (Hijmans et al., 2017). Initial models were fitted without correction for sampling bias (modelbiased) under the point process framework, following Renner et al. (2015). As species occurrences are opportunistic, we accounted for spatial sampling bias using four methods (see Table 2 for a summary). First, assuming that site-accessibility is the main driver for spatial sampling bias in the data, we employed model-based bias correction (Warton et al., 2013) using distance to shore as a bias predictor. In this method, the distance to shore variable was used as one of the model predictors but was then fixed at an optimum accessibility value (distance = zero) during prediction (modelaccessibility), assuming all cells have perfect accessibility (El-Gabbas & Dormann, 2018a; Warton et al., 2013). This method does not require refitting the modelbiased: modelaccessibility is an extension from the modelbiased, with the only difference being how the distance to shore variable is manipulated during predicting habitat suitability. Second, we filtered duplicated occurrences in each cell, i.e., using only one occurrence per 10×10 km cell, yielding 972 unique cells with species sightings. The filtered sightings were then used with the same 14 environmental variables (Table 1) to calibrate the second models (modelrarefaction). Spatial filtering (or rarefaction) is commonly used in SDMs to correct for sampling bias and reduce the effect of spatial autocorrelation (Aiello-Lammens et al., 2015; Boria et al., 2014). Table 2: Overview of the fitted models, including model configuration and evaluation. This table further shows, for each model, the best combination of feature classes (FC) and regularization multiplier (RM) as estimated on spatial-block cross-validation, the training AUC, and the mean ± standard deviation of cross-validated testing AUC. FC: linear, ‘L’; quadratic, ‘Q’; hinge, ‘H’; product ‘P’; and threshold, ‘T’). Model Sightings Background locations Predictors FC RM Training AUC Testing AUC Modelbiased All All cells in the study area 14 environmental predictors (Table 1) LQHPT 4 0.898 0.805 ± 0.11 Modelaccessibility All All cells in the study area 14 environmental predictors (distance to shore is fixed to zero during prediction) LQHPT 4 0.867 0.764 ± 0.10 Modelrarefaction One sighting per cell All cells in the study area 14 environmental predictors LQHP 0.5 0.899 0.818 ± 0.07 ModeleffortTracks All All cells in the study area 14 environmental predictors + intensity of ship tracks (Figure S3; fixed at maximum value during prediction) LQHPT 4 0.884 0.746 ± 0.09 ModeleffortFW All Sampled in proportion to estimated fin whale sampling intensity (Figure S3) 14 environmental predictors LQHPT 3 0.889 0.798 ± 0.11 For the other two bias correction methods, we estimated a pattern of spatial sampling efforts in the study area using the intensity of ship tracks or the intensity of fin whale sightings. Ship track data between 2004 and 2021 (May-September) were extracted from the sailwx database. The number of quality-controlled ship tracks intersected with each cell was calculated (log10 scale; Figure S3) and used as an additional bias predictor to the models (modeleffortTracks), implementing model-based bias correction. To predict from modeleffortTracks, the ship track bias predictor was fixed at the maximum ship track intensity in the study area (following El-Gabbas & Dormann, 2018a), assuming that all cells received similarly high sampling efforts. Finally, we used the intensity of fin whale sightings in each cell as a bias grid (~ bias file) to sample background locations with similar spatial bias as fin whale sightings (modeleffortFW) (Merow et al., 2013). As most cells lack species sightings, we cannot use sighting intensity map directly as a bias grid. We used fin whale sighting coordinates to calculate a two-dimensional kernel density estimation using MASS R-package (kde2d function; Venables & Ripley, 2002; see Figure S3). For all the models, all cells in the study area were used as background information, except for the modeleffortFW in which background locations were sampled as 20,000 cells (5,000 from each spatial cross-validation fold, see below) using the fin whale sighting intensity as sampling weight (using 'randomPoints' function from the raptr R-package, Hanson et al., 2017). Evaluating SDM performance typically requires independent datasets. As such dataset is unavailable in most situations, we used spatial-block cross-validation to ensure spatial independence between the training and testing dataset (Roberts et al., 2017). We used blockCV R-package (Valavi et al., 2019) to determine the block size and distribute blocks into four-fold cross-validation. Block size was estimated as the median spatial autocorrelation range of environmental variables, while the allocation of blocks into cross-validation folds was estimated by balancing the number of presence and background locations between folds. We determined two spatial block structures, one for modelrarefaction and another for other models (Figure S4). Model performance was evaluated using the area under the ROC curve (AUC) by comparing the ranking of predicted habitat suitability values at testing presences against predicted values at background locations in testing blocks (i.e., testing AUC). MaxEnt’s default settings were originally tuned using empirical data (Phillips & Dudik, 2008); therefore, optimum settings can vary between species, characteristics of species and environmental data, and study areas (Radosavljevic & Anderson, 2014). Thus, we tuned MaxEnt’s settings, estimating the best combination of feature classes (transformations of variables) and regularization multiplier (representing model complexity) using ENMeval R package (Muscarella et al., 2014). For each model type, a total of 40 submodels were calibrated on spatial-block cross-validation: combinations of five feature classes (linear, ‘L’; quadratic, ‘Q’; hinge, ‘H’; product, ‘P’; and threshold, ‘T’) × eight regularization multiplier values (from 0.5 to 4, with an 0.5 increment). For each model type, the combination with the highest cross-validated testing AUC was used to run the final models. In addition to cross-validated models, we also ran models with all respective sightings (referred to as ‘full models’). Predicted habitat suitability was made using the predict function of dismo R-package ('cloglog' output format, as recommended by Phillips et al., 2017). For cross-validated models, we calculated the mean habitat suitability and the coefficient of variation (a ratio between standard deviation and mean prediction) to represent predictive uncertainty. Variable importance was estimated using Jackknifing and MaxEnt’s permutation importance. We show how habitat suitability changes as each environmental variable is varied using marginal response curves. 3. Results All models showed good performance, with mean testing AUC ranging from 0.75 to 0.81 (training AUC from 0.87 to 0.9). Table S3 shows values of training AUC, the mean and standard deviation of cross-validated testing AUC, and the best combination for feature classes and regularization multiplier for each model. Important variables and marginal response curves show reasonably consistent patterns for the different bias correction methods. 3.1. Important variables The most important variables, as estimated with permutation importance, were distance to shore and distance to the sea ice edge, followed by the variability of temperature and salinity of the sea surface and depth (Figure 2). This is also supported by the jackknifing test (Figure 3 and S5). When used in isolation, the most important variables were distance to the sea ice edge and distance to shore (particularly for modeleffortFW), followed by the variability of sea surface temperature. Depending on the model type, model performance was lowest when depth, distance to shore, or distance to the sea ice edge was excluded (see Figures 3 and S5). Figure 2: Permutation importance (%) of environmental variables. Solid dots and their error bars represent the mean and standard deviation of importance on cross-validation, respectively. Asterisks represent the permutation importance of the full models (without cross-validation). Colors represent the four model types implemented (blue = modelbiased/accessibility, green = modelrarefaction, red = modele-ffortTracks, orange = modeleffortFW). Environmental variables are sorted in all figures in descending order according to their overall mean permutation importance. For more information on variable names, see Table 1. Figure 3: Variable importance as measured by Jackknifing test for modelbiased. The bars indicate mean regularized training gain for cross-validated models, with error bars for standard deviation. Results for the full model (without cross-validation) are shown as gray points. Blue bars represent the model gain when each variable was used in isolation, while red bars show model gain when models were run without the variable. For more information on variable names, see Table 1. Results for other model types are shown in Figure S5. 3.2. 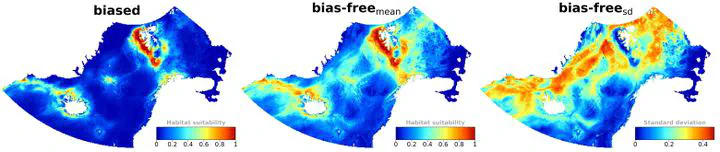Fin whale suitable habitats in the Nordic and Barents Seas The highest habitat suitability was predicted along the western coast of Svalbard and between Svalbard and the eastern Norwegian Sea, including southwestern parts of the Barents Sea. Comparably high habitat suitability areas include the area between the Knipovich Ridge and Jan Mayen (through Mohns Ridge) and Greenland’s southeastern coast up to around Iceland (including parts of the Denmark Strait) (Figures 4 and 5). Generally, bias-corrected predictions show expected broader habitat suitability compared to models that did not consider sampling bias correction (modelbiased; Figures 4 and 5). This is particularly evident for methods that implemented model-based bias correction (modelaccessibility and modeleffortTracks; Figure 5). The two other correction methods (modelrarefaction and modeleffortFW) show comparably less broad suitable habitats, more confined along the western coast of Svalbard and in the Barents Sea (Figure 5). The predictive uncertainty of cross-validated models (coefficient of variation) was generally low (Figure S6). Areas with relatively high cross-validated uncertainty include the northeastern coast of Greenland (70-81°N), southeast of the Barents Sea (35-45°E 64-70° N), southwest coast of Norway, and east of Iceland; areas not overlapping much with core suitable habitats (Figures 5 and S6). Figure 4: Fin whale habitat suitability in the Nordic and Barents Seas. The map to the left shows the mean predicted habitat suitability without correction for sampling bias (modelbiased). The other two maps show the mean and standard deviations (sd) of the four sampling bias correction methods, respectively. The mean predicted habitat suitability for each bias correction method is shown in Fig-ure 5. Colors range from blue (low suitability mean/sd) to red (high suitability mean/sd). Figure 5: Mean fin whale habitat suitability for each sampling bias correction method. The mean of the four maps (bias-free prediction) is shown in Figure 4. Similar maps representing model-specific coefficient of variation are shown in Figure S6. Marginal response curves for all environmental variables are shown in Figures 6 and S7. Here, only the environmental variables that were identified to be most important in the models (Figure 2) are described in detail. The highest habitat suitability was predicted at a distance <80 km to shore, then sharply declined. Models showed a unimodal relationship between fin whale habitat suitability and distance to the sea ice edge, peaked at ~100-200 km from the sea ice edge in ice-free areas, and then decreased sharply at higher distances. Habitat suitability was particularly low in ice-covered regions north of the sea ice edge. The response curves for sea ice concentration support these results, with the highest habitat suitability at low values (< 20%, Figure 6). Models showed a peak habitat suitability at around 200-300 m depth, with much lower suitability in very shallow or deep areas (Figure 6). There was no effect of mean salinity at 100 m up to a value of ~33.5 (although with high variability between models), above which habitat suitability increased (peaked at ~35) and then sharply decreased again (Figure 6). The highest fin whale habitat suitability was predicted at locations with low variability of temperature (sd <1.4°) or salinity (0.1-0.4) on the sea surface. Habitat suitability increased with slope values between 1° and 3° and stabilized at high slope values (Figure 6). Figure 6: Marginal response curves of environmental variables. Solid lines represent the mean re-sponse curve of cross-validated models; dashed lines for full models (without cross-validation). Line colors represent the model type used. The upper gray ticks show values of environmental conditions at species occurrences, while lower gray ticks are for values at the whole study area (background information). Environmental variables are sorted in descending order according to their overall mean permutation importance (Figure 2). Response curves for each model type, including cross-validation uncertainty, are shown in Figure S7. 4. Discussion Information on the spatiotemporal distribution and habitat preference of marine species is decisive for conservation planning and management. However, such data remains underrepresented, particularly from polar regions (Hammond et al., 2013; Redfern et al., 2006; Williams et al., 2006). Recent studies demonstrated the promising application of SDMs for conservation, decision-making, and dynamic management in the marine realm (e.g., Hazen et al., 2018), with a particular interest in using presence-only SDMs (El-Gabbas et al., 2021a; Smith et al., 2021). This study employed presence-only static SDMs (MaxEnt) to predict fin whales’ habitat suitability and niche preferences on their feeding grounds in the Nordic and Barents Seas. MaxEnt parameters and spatially independent model evaluation were estimated using spatial-block cross-validation. Recent studies have shown that the application of spatially independent model evaluation and correction for sampling bias is necessary to maximize the robustness of presence-only SDMs for conservation planning (Smith et al., 2021). To account for this, we implemented four methods to correct for spatial sampling bias. Our models showed high performance: high mean and little variability (low standard deviation) of testing AUC (Table S3) and low predictive uncertainty (Figure S6). 4.1. Fin whale potential distribution in the Nordic and Barents Seas Few studies have modeled the distribution of fin whales in the Nordic and Barents Seas. Recently, Storrie et al. (2018) modeled fin whale distribution around the Svalbard Archipelago, and the pattern of habitat suitability in their study largely agrees with our results. This area was predicted as highly suitable in all of our models (Figures 4 and 5). Skern-Mauritzen et al. (2011) revealed that fin whales occupy a narrow area along and north of the Polar Front in the Barents Sea. Our predictions agree with this to some extent: high habitat suitability is predicted in the proximity of the Polar Front in western parts of the Barents Sea and the western coast of Svalbard (Figures 1 and 4). This may point out potential feeding hotspots in this area, as fin whales and their prey have been observed previously within these areas (Kovacs et al., 2009; Skern-Mauritzen et al., 2011; Storrie et al., 2018). Our models predict high habitat suitability in the southwestern Barents Sea and along the Knipovich Ridge towards Jan Mayen (through the Mohns Ridge; Figure 4). The Knipovich Ridge is a biologically highly productive area featuring various prey species, including those of fin whales (Bonecker et al., 2014; Fock et al., 2004). Former studies suggested that the Knipovich Ridge is a seasonally important habitat for cetaceans, in which fin whales have been observed feeding (Nieukirk et al., 2004; Waring et al., 2008). Unsurprisingly, Storrie et al. (2018) reported many fin whale observations along the Knipovich Ridge, which is also depicted in the sighting data available to us (Figure 1). Likewise, high concentrations of fin whales around Jan Mayen (Moore et al., 2019; Nøttestad et al., 2014). Areas off Jan Mayen are known for their high densities of capelin (Mallotus villosus), krill, amphipods, and other fin whales’ planktonic prey species (Nøttestad et al., 2014; Vilhjálmsson, 2002), which can explain the high suitability of fin whales in this area (Nøttestad et al., 2014). Previous studies reported fin whale occurrences in East Greenland waters (Hansen et al., 2019; Heide-Jørgensen et al., 2007; Víkingsson et al., 2013b; Víkingsson et al., 2015). Nevertheless, our models predicted relatively low habitat suitability along the East Greenland coast compared to the Svalbard area, except in the southern part of the East Greenland coast (including parts of the Irminger Sea and south of the Denmark Strait; 60-65°N; Figures 4 and 5). This is consistent with the predictions of Víkingsson et al. (2015) and and available sightings used in this study (Figures 1 and S8). Without dedicated surveys, it is difficult to ensure if the low habitat suitability along the eastern coast of Greenland is due to a real low habitat preference or low sampling effort in this area. In future SDM studies, additional data (e.g., from the NAMMCO ‘North Atlantic Marine Mammal Commission’ surveys, unavailable to us) is necessary to improve habitat suitability predictions in the East Greenland area. 4.2. Fin whale habitat preferences 4.2.1. Distance to shore Distance to shore was among the two most important environmental variables in our models, with a clear habitat preference of fin whales for locations closer to shore (up to approx. 80 km) than farther away (Figures 2, 6, S7, and S9). Distance to shore was the most important variable in Storrie et al. (2018)’s modeling study around Svalbard, with deep areas beyond the continental slope predicted as highly unsuitable. Although our data may show spatial sampling bias towards more accessible areas, we should not neglect that the high importance of distance to shore may be related to ecological factors, such as high prey densities along the shelf off Norway and in the Barents Sea (for details, see Loeng & Drinkwater, 2007). 4.2.2. Sea ice Fin whales are mostly absent in densely ice-covered areas in the Arctic, and a negative correlation between fin whale calls and sea ice concentrations has been noted at both poles (Simon et al., 2010; Širović et al., 2004). In concordance, our results show high habitat suitability at 100-200 km distance from the sea ice edge in ice-free water and at locations with low (<20%) sea ice concentration (Figure 6). At low sea ice concentration values (up to 20%), modelrarefaction and modeleffortFW show a positive relationship, indicating some sea ice tolerance. This agrees with previous observations of fin whales in areas with loose drift ice and the modeled unsuitability in dense ice-covered areas in the Svalbard Archipelago (Storrie et al., 2018). Tsujii et al. (2016) suggested that fin whales arrive in the Pacific sector of the Arctic after sea ice melting and elevated water temperature. This supports our results, suggesting a temporal matching between fin whale migration into and from the Arctic and sea ice melting and formation. However, Edwards et al. (2015) indicated some fin whales remaining at higher latitudes throughout colder months, possibly further suggesting some sea ice tolerance to a certain extent. Sea ice has substantially decreased in the Arctic during recent decades (Overland & Wang, 2013). Future sea ice changes, and corresponding changes in the location of the sea ice edge, will likely affect fin whale habitat suitability in the Arctic, potentially leading to more open water areas accessible for the species. Climate change is expected to cause a shift in the abundance and availability of fin whales’ prey (Ahonen et al., 2021), and fin whales may respond to future climate change by extending their stay on polar feeding grounds, either spatially by occupying areas currently unavailable or temporally by prolonging their stay (Ahonen et al., 2021; Moore et al., 2019; Woodgate et al., 2015). Recently, fin whales have been increasingly sighted at novel places in the Arctic, particularly inside fjords of the Svalbard Archipelago (Vacquié-Garcia et al., 2017). 4.2.3. Water temperature High fin whale habitat suitability was predicted at locations with low variability in water temperature (<1.4 °C), then sharply declined at higher temperature variability, particularly on the surface (Figure 6 and S7). This suggests fin whale habitat preference to areas with homogenous temperatures during the summer months, which can also be linked to high habitat suitability at low sea ice concentrations in summer, as shown above. Víkingsson et al. (2015) found that sea surface temperature is one of the important variables for fin whale encounters in Icelandic waters, with high probability at a sea surface temperature range of 5°C–11°C, peaking at 6°C-7°C and similarly Skern-Mauritzen et al. (2011) found highest fin whale densities in sea surface temperature of ca. 6°C in the Barents Sea. Two recent modeling studies using satellite tracking data revealed that fin whales migrating from and to our study area prefer areas with low sea surface temperatures (<10°C) (Lydersen et al., 2020; Pérez-Jorge et al., 2020). In this study, variables presented mean water temperature (surface and 100 m depth) were excluded from model calibration due to a high correlation with other predictors. Particularly, they are positively correlated with distance to the sea ice edge and negatively correlated with mean sea ice concentration and the variability of sea surface salinity (Figure S9). However, most fin whale sightings were collected at mean sea temperature values between 4°C and 7°C, peaking at around 6°C (Figure S10). Our models support that fin whales may prefer a narrow range of sea surface temperature (Lydersen et al., 2020; Víkingsson et al., 2015) and low seasonal temperature variability. This is especially interesting in the light of rapidly rising water temperatures in the Arctic Ocean (Alexander et al., 2018). Rising water temperatures (~ sea ice loss) and the concomitant shift in prey species may explain the recent northward range expansion of seasonally resident cetaceans, including fin whales, in the Nordic Seas and around the Svalbard Archipelago (Kovacs et al., 2010; Storrie et al., 2018). The northward shift of fin whales might be facilitated due to certain flexibility in prey choice (Storrie et al., 2018) and the increased prey abundance, such as krill (Buchholz et al., 2012) and boreal fish species, through a northward expansion of their distribution (Berge et al., 2015; Fossheim et al., 2015; Kortsch et al., 2015). Such a change has already been reported for common minke whales (Balaenoptera acutorostrata) in Icelandic waters (Víkingsson et al., 2013a). It is important to highlight that our estimation of seasonal variability of water temperature was derived from monthly climatological data. In contrast to other dynamic predictors which are available at high temporal resolution (1-8 days), the original data on temperature (Locarnini et al., 2018) and salinity (Zweng et al., 2018) were obtained from the World Ocean Atlas 2018 at low spatiotemporal resolution (Table 1): a single map for each month at a resolution of 0.25° representing the mean value in the respective month over the period from 2005 to 2017. We calculated the variability (standard deviation) from monthly mean climatological maps for May to September (i.e., only five maps), which may indicate that much of the underlying seasonal variability is not captured in our calculations. Our estimated water temperature variability can be interpreted as the variability between monthly climatological mean temperatures, ignoring variability between years and within months. This may lead to an under- or overestimation of the importance and effect of these variables. Future data on water temperature at higher spatiotemporal resolution is necessary to further evaluate the validity of our results. 4.2.4. Salinity Interestingly, models show higher importance of the variation in sea surface salinity on fin whale habitat suitability than the mean salinity at 100 m depth (Figure 2). High habitat suitability is predicted at low variability of sea surface salinity (ca., 0.2 to 1.5), which was also reflected in available observations (Figures 6, S7, and S10). Fin whale habitat suitability peaked at high mean salinity at 100 m and low variability of sea surface salinity (Figure 6 and S7). At mean salinity values <33.5, models suggest no relationship between fin whale habitat suitability and salinity, although with different values of predicted habitat suitability for different models. The areas near the coast at the northwestern Greenland Sea and southern Barents Sea show low mean and high variability of salinity (Figure S2), which may explain the low fin whales’ habitat suitability at these areas (Figures 4, 5, and S2). The exact role of salinity on fin whale habitat preference remains unclear, though salinity is suggested to act as an indicator for upwelling and a proxy for associated high productivity (Falk-Petersen et al., 2015; Moore et al., 1995; Redfern et al., 2017; Tsujii et al., 2016). Further studies are needed to clarify the role of salinity on the distribution of fin whales in the Nordic and Barents Seas, particularly in light of the low spatiotemporal resolution of the original salinity data. 4.2.5. Ocean topography Depth and slope have been identified as important environmental variables of fin whale distribution in the North Atlantic, with high habitat suitability in steep and deep regions (Schleimer et al., 2019; Storrie et al., 2018; Woodley & Gaskin, 1996). Our models show low-to-moderate importance of both predictors (Figure 2). Models predict high habitat suitability in areas of >3° slope (Figure 6), revealing a preference of fin whales for relatively steeper areas, i.e., areas with some topographic variability. Indeed, Woodley and Gaskin (1996) observed that fin whales tend to aggregate where bottom topography is heterogeneous. Abrupt or steep depth changes are linked to local upwelling and fronts in some regions, which may enhance prey availability (Ingram et al., 2007; Woodley & Gaskin, 1996 and references therein). As marine mammal distribution on feeding grounds is directly linked to feeding resources, high habitat suitability in these areas is a reasonable consequence (Breen et al., 2016). It was found that fin whales utilize currents modulated by sea bottom topography (Panigada et al., 2005; Woodley & Gaskin, 1996), which may provide another explanation for fin whale distribution in steeper regions of the study area. For depth, we found a preference of fin whales towards comparably shallow areas: our models predicted peak habitat suitability at a depth of ca. 200 m, with a decreasing, yet comparably high, habitat suitability at depths up to 1,000 m (see Figure S7 and S10). Our results reflect those of Storrie et al. (2018), who found that fin whales in the study area ranged a broad array of depths, with a median depth of 250 m, and a maximum of 2,000 m. Fittingly, Lydersen et al. (2020) and Pérez-Jorge et al. (2020) reported that fin whales favored habitats <3,000 m deep around Svalbard and in the mid-North Atlantic Ocean, respectively. However, varying time spans, seasons (ranging from spring to autumn), and boundaries of the study area in different studies also may have an effect on the estimated preferred depth ranges. 4.3. Spatial sampling bias correction Sampling bias has been shown to affect model performance and interpretation and should be carefully considered when signs of spatial bias exist (El-Gabbas & Dormann, 2018a; Fithian et al., 2015; Fourcade et al., 2014; Phillips et al., 2009; Warton et al., 2013). Failure to eliminate sampling bias, particularly in environmental space, can lead to the suboptimal use of SDMs for conservation prioritization and inefficient use of limited conservation resources (El-Gabbas et al., 2020; Grand et al., 2007). In this study, we considered four methods for spatial sampling bias correction. The four methods show consistent variables’ importance and species responses to environmental changes (Table 2; Figures 2, 3, S5, and S7), demonstrating stable results. Sampling bias corrections led to broader areas of suitable habitats compared to models without bias correction (modelbiased; Figures 4 and 5). This is expected after bias correction, as bias correction leads to higher habitat suitability in undersampled areas (El-Gabbas & Dormann, 2018a; Warton et al., 2013). However, methods implemented model-based bias correction (Warton et al., 2013) (modelaccessibility and modeleffortTracks) show much broader high habitat suitability areas than modelrarefaction and modeleffortFW (Figures 4-5). Our use of ship tracks as bias predictor (modeleffortTracks) assumes that the pattern of ship tracks (Figure S3) reflects the spatial sampling bias in fin whales sightings, which may not necessarily be correct; i.e., they may reflect activities in the study area not directly related to fin whale sampling. Distance to shore was the most important variable in all models, irrespective of the bias correction method implemented (Figure 2). This supports our assumption of using accessibility as a driver of spatial bias in the highly remote Nordic and Barents Seas (modelaccessibility). Available sightings are spatially non-independent and opportunistic (Figure 1 and S8), observed mainly from touristic and small research vessels. These vessels are often limited to nearshore rather than offshore routes in the Arctic for safety, logistic, and financial reasons (Storrie et al., 2018; Vacquié-Garcia et al., 2017). However, distance to shore may also be correlated with (a proxy for) other (unknown) ecologically significant predictors not used in the model. In such a case, it is challenging to correct for sampling bias using opportunistic presence-only data alone (Fithian et al., 2015). In other words, we cannot be sure if the importance of distance to shore in our models was due to sampling bias towards the shore or an ecological signal confounded with spatial bias. Differences in predicted habitat suitability between different bias correction methods (Figure 5) suggest that using a single bias correction method may not be sufficient to ensure sampling bias correction. In our models, the use of model-based bias correction (modelaccessibility and modeleffortTracks (Warton et al., 2013) led to much broader patterns of habitat suitability as compared to the other two bias correction methods. However, it is challenging to determine from the currently available dataset which method is more successful in bias correction and whether descrepancies in predicted patterns of habitat suitability are mainly due to methodological reasons. For example, in model-based bias correction, bias predictors (here, distance to shore and the intensity of ship traffic) are assumed to be independent from environmental drivers affecting species distribution (Fithian et al., 2015; Warton et al., 2013), which can be challenging as discussed above. The pattern of predicted habitat suitability can also be sensitive to the value at which the bias predictors are fixed during prediction (El-Gabbas et al., 2021b). In other words, we can not ensure wether the prediction maps employing the model-based bias correction method overpredict fin whale suitable habitats or describe a better representation of fin whale habitat suitability in the Nordic and Barents Seas. In presence-only SDMs using opportunistic sightings, the reason for sampling bias is typically unknown, and the success of bias correction highly depends on how reasonable is the analyst’s expectation of the source of sampling bias. Evaluating bias correction success requires the availability of independent unbiased presence-absence testing data, which is not available in most situations (El-Gabbas & Dormann, 2018a; Phillips et al., 2009), particularly in polar regions. To avoid the potential sensitivity of our results on the choice of bias correction method, we used an ensemble (mean) of bias-free predictions from the four methods to represent a mean bias-free predicted habitat suitability of fin whales in the Nordic and Barents Seas. 4.4. Limitations Despite the high performance of the models and consistent results using four methods for correction for sampling bias, a few methodological and data limitations must be acknowledged. Our models are static, in which fin whale presence-only sightings were related to variables summarizing the environmental conditions during the feeding season over ~15 years (Table 1). The implemented static models assume that cells occupied with any fin whale sightings represent a suitable habitat during the entire feeding season and ignore possible changes or shifts in fin whale distribution through time (Bateman et al., 2012; El-Gabbas et al., 2021a, 2021b). Further, our static models can only describe persistent, broad-scale (macroscale) associations between fin whales and long-term characteristics of the ocean’s climate. Nevertheless, we also included variables representing environmental variability (standard deviation) during the feeding season to account for seasonal variability, capture extreme conditions unlikely to be captured in mean variables, and reduce the impact of temporal mismatching between sightings and environmental conditions (El-Gabbas et al., 2021b; Zimmermann et al., 2009). However, in order to capture ephemeral or contemporaneous processes and implement effective dynamic ocean management, dynamic SDMs are necessary (Becker et al., 2016; El-Gabbas et al., 2021a; Mannocci et al., 2017). Maintaining spatiotemporal matching between sightings and contemporaneous environmental conditions, necessary in dynamic models, requires the availability of environmental predictors at high spatiotemporal resolutions (e.g., daily or weekly; El-Gabbas et al., 2021b; Mannocci et al., 2017) and the availability of temporally unbiased species sightings (El-Gabbas et al., 2021b; Milanesi et al., 2020). However, some important environmental predictors are not available at high spatiotemporal resolution (e.g., salinity) or not available at all (e.g., prey abundance) (El-Gabbas et al., 2021b; Fernandez et al., 2017), making it challenging to spatiotemporally match sightings with contemporaneous environmental conditions. A common limitation to marine SDMs is the lack of information on the distribution of prey abundance at appropriate spatiotemporal resolutions (Robinson et al., 2011). A recent study by Schleimer et al. (2019) found a positive correlation between krill biomass and fin whale abundance in the North Atlantic. However, predator-prey associations are scale-dependent (Fall & Skern-Mauritzen, 2014). Therefore, the availability of prey abundance data at high spatiotemporal resolution seems necessary in future SDMs on cetaceans in the Nordic and Barents Seas. A related issue is that the environmental predictors we used were available at inconsistent spatiotemporal resolutions, which may affect the model outputs. The spatial resolution of the predictors ranges from coarse (0.25° for sea surface height, current speed, temperature, and salinity) to fine (e.g., depth: 30 arcseconds) spatial resolutions (Table 1). As it is necessary to run the models using environmental variables at consistent spatial resolutions, we compromised between available spatial resolutions and projected all variables into a 10×10 km grid. This interpolation process can lead to uncertainties, e.g., losing important information during averaging environmental conditions from fine to coarse resolutions (e.g., depth). Furthermore, the original predictors were available at different temporal resolutions, ranging from daily (e.g., sea ice concentration) to climatological monthly mean (salinity and temperature; Table 1), which makes the interpretation of variables representing environmental variability inconsistent between predictors. The influence of using environmental variables at different spatiotemporal resolutions needs further investigation in future studies. 4.5. Future implications In this study, we used MaxEnt, one of the most often applied presence-only SDM methods in terrestrial and marine environments (Fourcade et al., 2014; Melo-Merino et al., 2020). This study supports the use of opportunistic data and presence-only models to model highly mobile cetacean species in remote areas like the Arctic. Although our models show good performance and consistent results, we emphasize that sampling bias correction cannot be guaranteed (El-Gabbas & Dormann, 2018b). Therefore, obtaining more sightings from undersampled areas (such as the Irminger and Greenland Seas) and improving data accessibility and sharing (e.g., including NAMMCO dataset in future studies) should be of priority to improve the robustness of future SDM studies in the Arctic. Our results reinforce the valuable information provided from citizen science biodiversity repositories (e.g., GBIF and OBIS) to study cetacean distribution (e.g., Beck et al., 2014b; Bruce et al., 2014). Thus, it is crucial to maintain and improve the data quality of these repositories for future modeling applications. Nevertheless, it seems outstanding to complement open-access repository data with dedicated surveys, particularly from less-covered locations, to reduce the sampling bias in the data and improve model fit (Beck et al., 2014a; El-Gabbas & Dormann, 2018a). Predicted habitat suitability maps in our study could be used for planning future surveys. Improving the spatiotemporal resolution of environmental data is of mutual importance in future SDM applications. Obtaining high-resolution data will help avoid potential uncertainty resulting from using variables at different spatiotemporal resolutions and further enable the use of these environmental data to calibrate dynamic models. 4.6. Conclusions During recent decades, species distribution models have become a powerful tool for modeling habitat suitability of marine species, including mammals (Melo-Merino et al., 2020; Redfern et al., 2006; Robinson et al., 2011). They can act as an adequate planning tool for conservation by revealing environmental factors affecting cetaceans’ distribution and improving our understanding of the influence of climate change. In practice, this can be achieved by prioritizing areas for conservation, such as the identification of marine protected areas (MPAs) (Bailey & Thompson, 2009), guiding future seismic surveys (Bombosch et al., 2014), and diagnosing potential impacts before occurring (Marshall et al., 2014). This is especially valuable for the hard-to-access yet vulnerable Arctic Ocean. Observed climate changes, such as increasing sea temperatures or declining sea ice extent (e.g., Overland & Wang, 2013; Pistone et al., 2014; Stroeve et al., 2012), may affect cetacean distribution in the Arctic Ocean (Moore et al., 2019). SDMs may aid in mitigating the effects of the concomitant increased anthropogenic impact by protecting frequented areas. This could notably benefit fin whale populations, which are exposed to various impacts, amongst others ship strikes (Cates et al., 2017) and noise pollution (Castellote et al., 2012). We used presence-only SDMs to model fin whales’ distribution and habitat preference in the Nordic Seas, where whale sightings are particularly scarce and spatially biased due to safety, logistic, and financial reasons. Our models shed light on the particular importance of distance to shore and distance to the sea ice edge on the distribution of fin whales on their feeding grounds in the Nordic and Barents Seas. Other important variables were the variability of sea temperature and salinity and depth. The main suitable habitats that were identified were along the western coast of Svalbard, between Svalbard and the eastern Norwegian Sea, coastal areas off Iceland and southern East Greenland, and along the Knipovich Ridge. Our study supports the promising use of presence-only SDMs as a cost-effective tool to aid conservation decision-making processes. Further, SDM outputs can support the sustainable use of fisheries, planning for future biodiversity and seismic surveys, and avoid bycatch of species at conservation risk (Bombosch et al., 2014; Hazen et al., 2018). We emphasized that for effective presence-only models, robust model validation using spatially independent data sets and correction for sampling bias is necessary (El-Gabbas & Dormann, 2018a; Smith et al., 2021). We used spatial block cross-validation for spatially independent model evaluation and four methods to correct for sampling bias. Results of different bias correction methods were generally very similar, supporting our approach to accounting for sampling bias. Acknowledgments We thank the captains and nautical officers of RV Polarstern for collecting fin whale sighting data and other data providers, including GBIF and iOBIS. We further thank Andy Traumüller for his assistance with preparing environmental variables and organizing ship track data. We thank Hal Mueller for making sailwx ship tracks data (https://www.sailwx.info/) available to us. We are grateful to Helmut Hillebrand for the supervision of the master thesis underlying this publication. We appreciate the valuable comments from Marcus Huntemann on land-spillover at sea ice concentration data and Olaf Boebel and Ilse van Opzeeland for their helpful ideas on the analysis. We also thank three anonymous reviewers for their comments and feedback which have substantially contributed to the improvement of this paper. Author Contributions Diandra Duengen: Conceptualization; data curation; software; formal analysis; methodology; investigation; writing–original draft; writing–review and editing. Elke Burkhardt: Resources; supervision; writing–review and editing. Ahmed El-Gabbas: Conceptualization; data curation, software; formal analysis (lead); methodology (lead); investigation; visualization; supervision; writing–review and editing (lead). Table S1: Reference list of RV Polarstern cruises with fin whale sightings used in this study. Cruise Details PS 115/1 Burkhardt E (2020) Whale sightings during Polarstern cruise PS115/1. PANGAEA. https://doi.org/10.1594/PANGAEA.924582 PS 115/2 Burkhardt E (2020) Whale sightings during Polarstern cruise PS115/2. PANGAEA. https://doi.org/10.1594/PANGAEA.924569 PS 108 Burkhardt E (2020) Whale sightings during Polarstern cruise PS108 (ARK-XXXI/3). PANGAEA. https://doi.org/10.1594/PANGAEA.924585 PS 107 Burkhardt E (2020) Whale sightings during Polarstern cruise PS107 (ARK-XXXI/2). PANGAEA. https://doi.org/10.1594/PANGAEA.924587 PS 100 Burkhardt E (2020) Whale sightings during Polarstern cruise PS100 (ARK-XXX/2). PANGAEA. https://doi.org/10.1594/PANGAEA.924701 PS 99/2 Burkhardt E (2020) Whale sightings during Polarstern cruise PS99.2 (ARK-XXX/1.2). PANGAEA. https://doi.org/10.1594/PANGAEA.924702 PS 99/1 Burkhardt E (2020) Whale sightings during Polarstern cruise PS99.1 (ARK-XXX/1.1). PANGAEA. https://doi.org/10.1594/PANGAEA.924703 PS 94 Burkhardt E (2020) Whale sightings during Polarstern cruise PS94 (ARK-XXIX/3). PANGAEA. https://doi.org/10.1594/PANGAEA.924704 PS 93/2 Burkhardt E (2020) Whale sightings during Polarstern cruise PS93.2 (ARK-XXIX/2.2). PANGAEA. https://doi.org/10.1594/PANGAEA.924705 PS 93/1 Burkhardt E (2020) Whale sightings during Polarstern cruise PS93.1 (ARK-XXIX/2.1). PANGAEA. https://doi.org/10.1594/PANGAEA.924706 PS 92 Burkhardt E (2020) Whale sightings during Polarstern cruise PS92 (ARK-XXIX/1). PANGAEA. https://doi.org/10.1594/PANGAEA.924707 PS 87 Burkhardt E (2020) Whale sightings during Polarstern cruise PS87 (ARK-XXVIII/4). PANGAEA. https://doi.org/10.1594/PANGAEA.924708 PS 86 Burkhardt E (2020) Whale sightings during Polarstern cruise PS86 (ARK-XXVIII/3). PANGAEA. https://doi.org/10.1594/PANGAEA.924709 PS 85 Burkhardt E (2020) Whale sightings during Polarstern cruise PS85 (ARK-XXVIII/2). PANGAEA. https://doi.org/10.1594/PANGAEA.924710 PS80/2 Burkhardt E (2021): Whale sightings during POLARSTERN cruise ARK-XXVII/2 (PS80/2). PANGAEA. https://doi.org/10.1594/PANGAEA.929095 PS 70 Burkhardt E (2020) Whale sightings during Polarstern cruise ARK-XXII/1c. PANGAEA. https://doi.org/10.1594/PANGAEA.924715 PS 70 Burkhardt E (2020) Whale sightings during Polarstern cruise PS ARK XXII/1a. PANGAEA. https://doi.org/10.1594/PANGAEA.924717 PS 72 Burkhardt E (2020) Whale sightings during Polarstern cruise ARK-XXIII/2. PANGAEA. https://doi.org/10.1594/PANGAEA.924713 Table S2: Variable transformations and variance inflation factor (VIF) values for final environmental variables used in the model (sd = standard deviation). For more information, see Table 1. Variable Transformation VIF Aspect 1.06 Bathymetry 3.27 Slope 1.17 Distance to Shore 2.82 Distance to 500 m isobath square root 3.53 SSH sd inverse 3.28 Current speed natural log 2.07 SIC 2.64 Distance to sea ice edge 2.59 Salinity 0 sd natural log 2.63 Salinity 100 m 2.18 Temp 0 sd 3.00 Temp 100 sd natural log 1.80 Chlorophyll-a sd 1.38 Figure S1: The number of quality-controlled fin whale sightings per year and month. Figure S2: Maps for the 14 environmental variables used in the models. The dashed line in the second map depicts the mean location of the sea ice edge during summer. See Table 1 for more information on data sources, units and spatiotemporal resolution of original environmental predictors. Figure S3: The estimated pattern of sampling efforts in the Nordic and Barents Seas. The first map represents the log10 number of ship tracks per cell (May to September 2004-2021). This map was used as a bias predictor in modeleffortTracks. The second map showed the kernel density estimate for fin whale sightings. This map was used in modeleffortFW as a bias grid; i.e., background locations are sampled from the study area using this layer as sampling weight. Figure S4: The spatial blocks used to cross-validate the models. The blocks to the left were used in all models, except for modelrarefaction, for which different blocks were estimated after removing duplicated sightings in each cell (right). Block size and how blocks were assigned to cross-validation folds were estimated using the blockCV R-package: 471.571 km for all models, except for modelrarefaction: 453.767 km. Figure S5: Variable importance as measured by Jackknifing test: a) modelrarefaction, b) modeleffortTracks; c) modeleffortFW. The bars indicate the mean regularized training gain for cross-validated models, with error bars for standard deviation. Blue bars represent the model gain when each variable was used in isolation, while red bars show model gain when models were used without the variable. Results for the full model (without cross-validation) are shown as gray points. For more information on variable names, see Table 1. Results for modelbiased / modelaccessibility are shown in Figure 3. Figure S6: Coefficient of variation of fin whale habitat suitability for each sampling bias correction method. The coefficient of variation represents the ratio between the mean and standard deviation of cross-validated habitat suitability. Low values (blue) indicate little cross-validation variability, while high values (red) indicate higher variability. Similar maps representing model-specific mean predicted habitat suitability are shown in Figure 5. Figure S7: Marginal response curves of environmental variables used in each model. Blue lines and their shaded areas represent the mean and standard deviation of response curves for cross-validated models; red lines for full models. The upper gray ticks show values at species sightings (see Figure S10), while lower gray ticks are for values in the whole study area (background information). Figure S8: Number of fin whale sightings per 50×50 km grid. Lightgray-colored areas are locations without any sightings. Dark gray areas represent land. Color ranges from yellow for low number of sightings to red for high number of sightings. Figure S9: Pairwise Pearson correlation coefficient between environmental variables. Colors range from red for high negative correlation (−1) to blue for high positive correlation (1). The larger is the point, the higher is the absolute value of correlation. The plot to the left shows results for the 24 initial variables. The bold black squares show the high correlation between mean water temperature and other predictors used in the models, explaining why variables for mean temperature were excluded from the models. The right plot shows results for the less correlated 14 environmental variables used to run the models. See Figure S2 and Tables 1 and S2 for more details. Figure S10: Histograms for values of environmental variables at fin whale sightings The 14 environmental variables used to run the models are marked with bold blue boxes. See Figure S2 and Tables 1 and S2 for more details.